题目内容
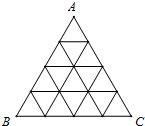 如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=
如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=考点:归纳推理,等差数列的前n项和
专题:综合题,推理和证明
分析:根据等差中项法分别求解n=2,3,4时的值,由此归纳出f(n)的值即可.
解答:
解:由题意可得,(各点放的数用该点的坐标表示)
当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1,2(D+E+F)=2(A+B+C)=2,D+E+F=1,∴f(2)=2=
,
当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1,从而可得D+E+H+I+F+F=2(A+B+C)=2,
同样根据等差中项可得,M的数为
,所以f(3)=3+
=
,
依次可知结论为f(n)=
,那么可知顶点A,B,C处的三个数互不相同且和为1,
则n=5时,所有顶点的数之和S=5,
故答案为:5.
当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1,2(D+E+F)=2(A+B+C)=2,D+E+F=1,∴f(2)=2=
| 3×4 |
| 6 |
当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1,从而可得D+E+H+I+F+F=2(A+B+C)=2,
同样根据等差中项可得,M的数为
| 1 |
| 3 |
| 1 |
| 3 |
| 4×5 |
| 6 |
依次可知结论为f(n)=
| n(n+1) |
| 6 |
则n=5时,所有顶点的数之和S=5,
故答案为:5.
点评:本题考查归纳推理,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
记F(x,y)=(x-y)2+(
+
)2(y≠0),则F(x,y)的最小值是( )
| x |
| 3 |
| 3 |
| y |
A、
| ||
B、
| ||
C、
| ||
| D、4 |