题目内容

求等差数列2，5，8，…，47中各项的和．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由题意可得等差数列的首项a1=2，公差d=3，共有n=16项，代求和公式计算可得．
解答： 解：由题意可得等差数列的首项a1=2，公差d=3，
∴an=2+3（n-1）=47，解得n=16，
∴各项的和S16=
16(2+47)
2
=392
点评：本题考查等差数列的求和公式，属基础题．
练习册系列答案
相关题目
甲、乙、丙、丁、戊五名应届师范毕业生分配到A，B，C三所学校任教，其中A学校和B学校要2人，C学校要1人，且甲、乙两人不能到同一所学校任教，则不同的分配方案的种数为（　　）
A、30B、48C、24D、36
在△ABC中，已知∠B=
π
3
．
（1）若b=
13
，a=3．求c；
（2）设t=sinAsinC，求t的最大值．
设函数f（x）是定义在R上的偶函数，且对任意的x∈R恒有f（x+1）=f（x-1），已知当x1，x2∈[0，1]且x1＜x2时，（x2-x1）[f（x1）-f（x2）]＞0，则有
①2是函数f（x）的周期；
②函数f（x）无最大值，有最小值是0；
③函数f（x）在（1，2）上是减函数，在（2，3）上是增函数；
④函数的对称轴x=k，k∈Z．
其中所有正确命题的序号是
 
．
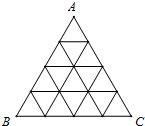如图，将正△ABC分割成16个全等的小正三角形，在每个三角形的顶点各放置一个数，使位于同一直线上的点放置的数（当数的个数不少于3时）都分别依次成等差数列，若顶点A，B，C处的三个数互不相同且和为1，则所有顶点的数之和S=
 
．
求导：y=
x+sinx
x-cosx
．
在0°～360°之间，分别找出与下列各角终边相同的角，并判断它们各是哪个象限的角：
（1）-45°        （2）760°
（3）-480°       （4）1230°．
在△ABC中，角A、B、C的对边分别为a、b、c，已知sinB=
5
13
，且b2=ac．
（1）求
sinB
sinAsinC
的值；
（2）若
BA
•
BC
=12，求b的值．
若某个几何体的三视图（单位：cm）如图所示，则该几何体的体积是（　　）
A、
2
12
cm3
B、
2
6
cm3
C、
2
3
cm3
D、
2
2
cm3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网