题目内容
某快递公司正在统计所有快递员某一天的收件数,有些数据还没有填好,如下表所示:
(1)求a,b,c的值,并估计当天收件数的中位数;
(2)若按分层抽样从四、五、六组中抽出6人进行经验交流,再从这6人中选取2人在公司早会上发言,求发言的2人不都是出自同一组的概率.
| 组别 | 分组(件数) | 频数 | 频率 |
| 一 | [50,60) | 1 | |
| 二 | [60,70) | c | |
| 三 | [70,80) | 10 | |
| 四 | [80,90) | b | 0.36 |
| 五 | [90,100) | 12 | |
| 六 | [100,110] | 6 | 0.12 |
| 合计 | a |
(2)若按分层抽样从四、五、六组中抽出6人进行经验交流,再从这6人中选取2人在公司早会上发言,求发言的2人不都是出自同一组的概率.
考点:列举法计算基本事件数及事件发生的概率,众数、中位数、平均数
专题:概率与统计
分析:(1)根据频率=
,分别求得a、b、c的值,再求出样本的中位数,即可估计估计当天收件数的中位数.
(2)根据分层抽样求出四、五、六组中被抽取的人数,6人为abcdef,记“发言的2人不都是出自同一组”为事件A,用列举法列举从6人中任取2人的所有情形,进而可得事件A所含的基本事件的种数,由等可能事件的概率,计算可得答案.
| 频数 |
| 样本容量 |
(2)根据分层抽样求出四、五、六组中被抽取的人数,6人为abcdef,记“发言的2人不都是出自同一组”为事件A,用列举法列举从6人中任取2人的所有情形,进而可得事件A所含的基本事件的种数,由等可能事件的概率,计算可得答案.
解答:
解:(1)0.12=
,解得a=50人,则b=0.36×50=18人,频率为c所对应的人数为50-(1+10+18+12+6)=3人,故c=
=0.06,
前三组人数为1+3+10=14人,后两组人数为12+6=18人,故中位数落在第四组,因为14+11=25,故中位数为80+
×10≈86
(2)读表可得,第四、五、六组组分别有18、12、6人,共36人,
要求从中用分层抽样法抽取6名学生,
则第四组抽出的人数为6×
=3人,用a、b、c表示,
第五组抽出的人数为6×
=2人,用d、e表示,
第六组抽出的人数为6×
=1人,用f表示,
则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}共有15种;
记“发言的2人不都是出自同一组”为事件A,则事件A所含的基本事件的种数有11种.
故P(A)=
| 6 |
| a |
| 3 |
| 50 |
前三组人数为1+3+10=14人,后两组人数为12+6=18人,故中位数落在第四组,因为14+11=25,故中位数为80+
| 11 |
| 18 |
(2)读表可得,第四、五、六组组分别有18、12、6人,共36人,
要求从中用分层抽样法抽取6名学生,
则第四组抽出的人数为6×
| 18 |
| 36 |
第五组抽出的人数为6×
| 12 |
| 36 |
第六组抽出的人数为6×
| 6 |
| 36 |
则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}共有15种;
记“发言的2人不都是出自同一组”为事件A,则事件A所含的基本事件的种数有11种.
故P(A)=
| 11 |
| 15 |
点评:本题主要考查频率分步表的应用,分层抽样、古典概率及其计算公式,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
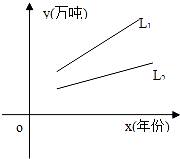 对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:
对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
(2)产品已出现了供大于求的情况,价格将趋跌;
(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;
(4)产品的产、销情况均以一定的年增长率递增.较合理的是( )
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
全集S={0,1,3,5,7,9},CSA={0,5,9},B={3,5,7}则A∩B=( )
| A、{3,5} | B、{3,7} |
| C、{3,5,7} | D、∅ |
已知函数f(x)=
是奇函数,则g(-4)的值等于( )
|
| A、-4 | B、-2 | C、2 | D、4 |
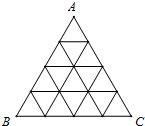 如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=
如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=