题目内容
已知函数f(x)=ex-2x,g(x)=x2+m(m∈R).设函数h(x)=af(x)-g (x),当a在区间[1,2]内变化时,若函数y=h(x),x∈[0,3]有零点,求实数m的最大值.
考点:函数的零点
专题:综合题,导数的综合应用
分析:根据根的存在性定理知 h(x)在[0,3]上的最大值与最小值要异号,从而找到m关于a的关系,得到m的最值.
解答:
解:∵由h(x)=a(ex-2x)-x2-m,
∴可得h′(x)=a(ex-2)-2x,
当x∈[0,ln2]时,ex-2<0,
∴x∈[0,ln2]时,y=h′(x)<0,
故?a∈[1,2],h(x)在x∈[0,ln2]为单调递减函数,
故函数h(x)max=h(0)=a-m;
当x∈[ln2,3]时,
∵ex-2>0,a∈[1,2],
∴h′(x)的值在区间[(ex-2)-2x,2(ex-2)-2x]上变化,
此时,对于函数 M(x)=2(ex-2)-2x,存在x0∈[ln2,3],M(x)在x∈[ln2,x0]单调递减,在x∈[x0,3]单调递增,
∴h(x)在x∈[ln2,3]的最大值为h(3)=a(e3-6)-9-m,
∵a∈[1,2],h(3)-h(0)=a(e3-7)-9>0,
∴h(3)>h(0),
因此h(x)的最大值是h(3)=a(e3-6)-9-m,
故当函数y=h(x)有零点时,a(e3-6)-9-m≥0
∵a∈[1,2],m≤2(e3-6)-9,
∴实数m的最大值是m=2(e3-6)-9=2e3-21.
∴可得h′(x)=a(ex-2)-2x,
当x∈[0,ln2]时,ex-2<0,
∴x∈[0,ln2]时,y=h′(x)<0,
故?a∈[1,2],h(x)在x∈[0,ln2]为单调递减函数,
故函数h(x)max=h(0)=a-m;
当x∈[ln2,3]时,
∵ex-2>0,a∈[1,2],
∴h′(x)的值在区间[(ex-2)-2x,2(ex-2)-2x]上变化,
此时,对于函数 M(x)=2(ex-2)-2x,存在x0∈[ln2,3],M(x)在x∈[ln2,x0]单调递减,在x∈[x0,3]单调递增,
∴h(x)在x∈[ln2,3]的最大值为h(3)=a(e3-6)-9-m,
∵a∈[1,2],h(3)-h(0)=a(e3-7)-9>0,
∴h(3)>h(0),
因此h(x)的最大值是h(3)=a(e3-6)-9-m,
故当函数y=h(x)有零点时,a(e3-6)-9-m≥0
∵a∈[1,2],m≤2(e3-6)-9,
∴实数m的最大值是m=2(e3-6)-9=2e3-21.
点评:本题考查了函数与方程的关系,以及利用导数讨论函数的最值.本题的难点是二元函数的转化问题,在二元函数转化时要先固定一个变量.求解本题要熟练掌握导数求最值的方法.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
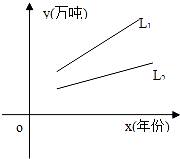 对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:
对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
(2)产品已出现了供大于求的情况,价格将趋跌;
(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;
(4)产品的产、销情况均以一定的年增长率递增.较合理的是( )
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
已知函数f(x)=
是奇函数,则g(-4)的值等于( )
|
| A、-4 | B、-2 | C、2 | D、4 |
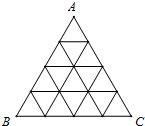 如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=
如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=