题目内容
求和:
+
+
+…+
.
| 1 |
| 4×12-1 |
| 1 |
| 4×22-1 |
| 1 |
| 4×32-1 |
| 1 |
| 4n2-1 |
考点:数列的求和
专题:计算题,点列、递归数列与数学归纳法
分析:由
=
=
(
-
),把要求和的每一项裂项后求和得答案.
| 1 |
| 4n2-1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:∵
=
=
(
-
),
∴
+
+
+…+
=
[(1-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=
(1-
)=
.
| 1 |
| 4n2-1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴
| 1 |
| 4×12-1 |
| 1 |
| 4×22-1 |
| 1 |
| 4×32-1 |
| 1 |
| 4n2-1 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-3 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题考查了裂项相消法求数列的前n项和,涉及等差数列相邻两项乘积的倒数数列的求和问题,常采用裂项相消法求和,是中档题.

练习册系列答案
相关题目
已知b为如图所示的程序框图输出的结果,则二项式(
-
)6的展开式中的常数项式( )

| bx |
| 1 | ||
|

| A、-20 | B、-540 |
| C、20 | D、540 |
甲、乙、丙、丁、戊五名应届师范毕业生分配到A,B,C三所学校任教,其中A学校和B学校要2人,C学校要1人,且甲、乙两人不能到同一所学校任教,则不同的分配方案的种数为( )
| A、30 | B、48 | C、24 | D、36 |
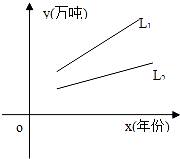 对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:
对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述: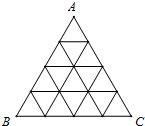 如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=
如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=