题目内容
已知函数f（x）是奇函数且f（log
4）=-3，当x＞0时，f（x）=ax（a＞0，a≠1），则实数a的值为（ ）
| 1 |
| 2 |
| A、9 | ||
| B、3 | ||
C、
| ||
D、
|
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：本题利用对数运算的性质和函数的奇偶性，将f（log
4）=-3转化为f（2）=3，再利用当x＞0时，f（x）=ax（a＞0，a≠1），从而求出a的值，得到本题结论．
| 1 |
| 2 |
解答：
解：∵函数f（x）是奇函数，
∴f（-x）=-f（x）．
∵f（log
4）=-3，
∴f（-log24）=-3，
∴f（-2）=-3，
∴f（2）=3．
∵当x＞0时，f（x）=ax（a＞0，a≠1），
∴a2=3，
∴a=
．
故选D．
∴f（-x）=-f（x）．
∵f（log
| 1 |
| 2 |
∴f（-log24）=-3，
∴f（-2）=-3，
∴f（2）=3．
∵当x＞0时，f（x）=ax（a＞0，a≠1），
∴a2=3，
∴a=
| 3 |
故选D．
点评：本题考查了，本题难度不大，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
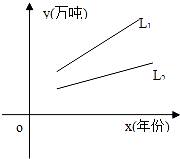对某种产品市场产销量情况如图所示，其中：L1表示产品各年年产量的变化规律；L2表示产品各年的销售情况．下列叙述：（1）产品产量、销售量均以直线上升，仍可按原生产计划进行下去；
（2）产品已出现了供大于求的情况，价格将趋跌；
（3）产品的库存积压将越来越严重，应压缩产量或扩大销售量；
（4）产品的产、销情况均以一定的年增长率递增．较合理的是（ ）
| A、（1）（2） |
| B、（2）（3） |
| C、（3）（4） |
| D、（1）（4） |
若不等式组
，表示的平面区域是一个锐角三角形，则实数k的取值范围是（ ）
|
| A、（-∞，-1） |
| B、（0，1） |
| C、（1，+∞） |
| D、（-1，0） |
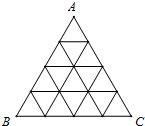如图，将正△ABC分割成16个全等的小正三角形，在每个三角形的顶点各放置一个数，使位于同一直线上的点放置的数（当数的个数不少于3时）都分别依次成等差数列，若顶点A，B，C处的三个数互不相同且和为1，则所有顶点的数之和S=