题目内容
三棱锥O-ABC中,OA=OB=OC=2,且∠BOC=45°,则三棱锥O-ABC体积的最大值是 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:将△BOC作为三棱锥的底面,当OA⊥平面BOC时,该棱锥的高最大,体积就最大,由此能求出三棱锥O-ABC体积的最大值.
解答:
解:将△BOC作为三棱锥的底面,
∵OA=OB=OC=2,且∠BOC=45°,
∴△BOS的面积为定值S=
×2×2×sin45°=
,
∴当OA⊥平面BOC时,该棱锥的高最大,体积就最大,
此时三棱锥O-ABC体积的最大值V=
×S×h=
×
×2=
.
故答案为:
.
∵OA=OB=OC=2,且∠BOC=45°,
∴△BOS的面积为定值S=
| 1 |
| 2 |
| 2 |
∴当OA⊥平面BOC时,该棱锥的高最大,体积就最大,
此时三棱锥O-ABC体积的最大值V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查三棱锥的体积的最大值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
在△ABC中,若|
+
|=|
-
|,AB=2,AC=1,E,F为BC边的三等分点,则
•
=( )
| AB |
| AC |
| AB |
| AC |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x3+g(x)+1,其中g(x)(x∈R)为奇函数,若f(a)=2,则f(-a)的值为( )
| A、-2 | B、-1 | C、0 | D、3 |
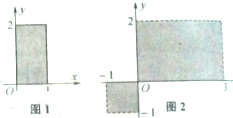 如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合:
如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合: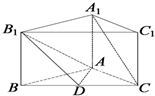 如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,
如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中, 如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为
如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为