题目内容
在△ABC中,若|
+
|=|
-
|,AB=2,AC=1,E,F为BC边的三等分点,则
•
=( )
| AB |
| AC |
| AB |
| AC |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的平方即为模的平方,可得
•
=0,再由向量的三角形法则,以及向量共线的知识,化简即可得到所求.
| AB |
| AC |
解答:
解:若|
+
|=|
-
|,
则
2+
2+2
•
=
2+
2-2
•
,
即有
•
=0,
E,F为BC边的三等分点,
则
•
=(
+
)•(
+
)=(
+
)•(
+
)
=(
+
)•(
+
)
=
2+
2+
•
=
×(1+4)+0=
.
故选B.
| AB |
| AC |
| AB |
| AC |
则
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
即有
| AB |
| AC |
E,F为BC边的三等分点,
则
| AE |
| AF |
| AC |
| CE |
| AB |
| BF |
| AC |
| 1 |
| 3 |
| CB |
| AB |
| 1 |
| 3 |
| BC |
=(
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
=
| 2 |
| 9 |
| AC |
| 2 |
| 9 |
| AB |
| 5 |
| 9 |
| AB |
| AC |
| 2 |
| 9 |
| 10 |
| 9 |
故选B.
点评:本题考查平面向量的数量积的定义和性质,考查向量的平方即为模的平方,考查向量共线的定理,考查运算能力,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
圆(x-2)2+(y-3)2=2的圆心坐标和半径长分别为( )
A、(2,3)和
| ||
B、(-2,-3)和
| ||
| C、(2,3)和2 | ||
| D、(-2,-3)和2 |

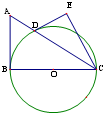 选修4-1:几何证明选讲
选修4-1:几何证明选讲