题目内容
已知函数f(x)=sinx-xcosx的导函数为f′(x).
(1)求证:f(x)在(0,π)上为增函数;
(2)若存在x∈(0,π),使得f′(x)>
x2+λx成立,求实数λ的取值范围;
(3)设F(x)=f′(x)+2cosx,曲线y=F(x)上存在不同的三点A(x1,y1),B(x2,y2),C(x3,y3),x1<x2<x3,且x1,x2,x3∈(0,π),比较直线AB的斜率与直线BC的斜率的大小,并证明.
(1)求证:f(x)在(0,π)上为增函数;
(2)若存在x∈(0,π),使得f′(x)>
| 1 |
| 2 |
(3)设F(x)=f′(x)+2cosx,曲线y=F(x)上存在不同的三点A(x1,y1),B(x2,y2),C(x3,y3),x1<x2<x3,且x1,x2,x3∈(0,π),比较直线AB的斜率与直线BC的斜率的大小,并证明.
考点:利用导数研究函数的单调性,导数的运算
专题:导数的综合应用
分析:(1)利用导数判断函数的单调性求出递增区间;
(2)转化为求函数的最大值问题解决,利用导数求出函数的最大值即得结论;
(3)利用导数的几何意义求出求出斜率,判断斜率的大小关系,得出结论.
(2)转化为求函数的最大值问题解决,利用导数求出函数的最大值即得结论;
(3)利用导数的几何意义求出求出斜率,判断斜率的大小关系,得出结论.
解答:
解 (1)证明:f′(x)=xsinx,
当x∈(0,π)时,sinx>0,所以f′(x)>0恒成立,
所以f (x) 在(0,π)上单调递增.
(2)因为f′(x)>
x2+λx,所以xsinx>
x2+λx.
当0<x<π时,λ<sinx-
x.
设φ(x)=sinx-
x,x∈(0,π),则φ′(x)=cosx-
.
当0<x<
时,φ′(x)>0;当
<x<π时,φ′(x)<0.
于是φ (x)在(0,
)上单调递增,在 (
,π)上单调递减,
所以当0<x<π时,φ(x)max=g (
)=
-
因此λ<
-
.
(3)由题意知只要判断
<
的大小.
首先证明:
<F′(x2).
由于x2<x3,因此只要证:F(x3)-F(x2)<(x3-x2) F′(x2).
设函数G(x)=F(x)-F(x2)-(x-x2) F′(x2)( x2<x<π),
因为F′(x)=xcosx-sinx=-f(x),所以G′(x)=F′(x)-F′(x2)=f (x2)-f (x),
由(1)知f(x)在(0,π)上为增函数,所以G′(x)<0.
则G(x)在(x2,π)上单调递减,又x>x2,故G(x)<G(x2)=0.
而x2<x3<π,则G(x3)<0,即F(x3)-F(x2)-(x3-x2) F′(x2)<0,即F(x3)-F(x2)<(x3-x2) F′(x2).
从而
<F′(x2)得证.
同理可以证明:F′(x2)<
.
因此有
<
,即直线AB的斜率大于直线BC的斜率.
当x∈(0,π)时,sinx>0,所以f′(x)>0恒成立,
所以f (x) 在(0,π)上单调递增.
(2)因为f′(x)>
| 1 |
| 2 |
| 1 |
| 2 |
当0<x<π时,λ<sinx-
| 1 |
| 2 |
设φ(x)=sinx-
| 1 |
| 2 |
| 1 |
| 2 |
当0<x<
| π |
| 3 |
| π |
| 3 |
于是φ (x)在(0,
| π |
| 3 |
| π |
| 3 |
所以当0<x<π时,φ(x)max=g (
| π |
| 3 |
| ||
| 2 |
| π |
| 6 |
因此λ<
| ||
| 2 |
| π |
| 6 |
(3)由题意知只要判断
| F(x3)-F(x2) |
| x3-x2 |
| F(x2)-F(x1) |
| x2-x1 |
首先证明:
| F(x3)-F(x2) |
| x3-x2 |
由于x2<x3,因此只要证:F(x3)-F(x2)<(x3-x2) F′(x2).
设函数G(x)=F(x)-F(x2)-(x-x2) F′(x2)( x2<x<π),
因为F′(x)=xcosx-sinx=-f(x),所以G′(x)=F′(x)-F′(x2)=f (x2)-f (x),
由(1)知f(x)在(0,π)上为增函数,所以G′(x)<0.
则G(x)在(x2,π)上单调递减,又x>x2,故G(x)<G(x2)=0.
而x2<x3<π,则G(x3)<0,即F(x3)-F(x2)-(x3-x2) F′(x2)<0,即F(x3)-F(x2)<(x3-x2) F′(x2).
从而
| F(x3)-F(x2) |
| x3-x2 |
同理可以证明:F′(x2)<
| F(x2)-F(x1) |
| x2-x1 |
因此有
| F(x3)-F(x2) |
| x3-x2 |
| F(x2)-F(x1) |
| x2-x1 |
点评:本题以三角函数为载体,考查导数的应用及分类讨论思想,适时结合形分析.其中第三问找一个中间量F′(x2),难度稍大.

练习册系列答案
相关题目
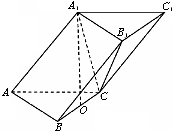 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=