题目内容
函数y=log
cos(
-2x)的单调递增区间是( )
| 1 |
| 2 |
| 3π |
| 2 |
A、[kπ-
| ||||
B、[kπ-
| ||||
C、[kπ+
| ||||
D、[kπ+
|
考点:复合函数的单调性
专题:三角函数的图像与性质
分析:利用诱导公式可得函数y=log
(-sin2x),令t=sin2x,则y=log
(-t),本题即求在满足t<0的条件下函数t的增区间,故有2kπ-
≤2x<2kπ,k∈z,解得x的范围,可得函数y的增区间.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
解答:
解:∵函数y=log
cos(
-2x)=log
(-sin2x),
令t=sin2x,则y=log
(-t),
本题即求在满足t<0的条件下函数t的增区间,
∴2kπ-
≤2x<2kπ,k∈z,解得 kπ-
≤x<kπ,
故函数y的增区间为[kπ-
,kπ)(k∈Z),
故选:B.
| 1 |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
令t=sin2x,则y=log
| 1 |
| 2 |
本题即求在满足t<0的条件下函数t的增区间,
∴2kπ-
| π |
| 2 |
| π |
| 4 |
故函数y的增区间为[kπ-
| π |
| 4 |
故选:B.
点评:本题主要考查复合函数的单调性,正弦函数的图象和性质,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
下列命题中,真命题的个数有( )
①?x∈R, x2-x+
≥0;
②?x>0, lnx+
≤2;
③“a>b”是“ac2>bc2”的充要条件;
④y=x|x|是奇函数.
①?x∈R, x2-x+
| 1 |
| 4 |
②?x>0, lnx+
| 1 |
| lnx |
③“a>b”是“ac2>bc2”的充要条件;
④y=x|x|是奇函数.
| A、1个 | B、2个 | C、3个 | D、4个 |
设集合S={0,a},T={x∈Z|x2<2},则“a=1”是“S⊆T”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
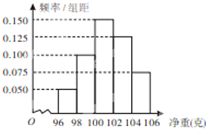 给出下列五个命题:
给出下列五个命题: