题目内容
14.在复平面内,M、N两点对应的复数分别为1-3i、-2+i,则|MN|=( )| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | 5 |
分析 直接利用复数对应点的坐标,求解距离即可.
解答 解:在复平面内,M、N两点对应的复数分别为1-3i、-2+i,
可得复数1-3i和-2+i对应的点为(1,-3),(-2,1),
则|MN|=$\sqrt{(1+2)^{2}+(-3-1)^{2}}=5$.
故选:D.
点评 本题考查复数与复平面之间的点的坐标的对应关系,两点间的距离公式的应用,是基础题.

练习册系列答案
相关题目
5.由曲线y=2$\sqrt{x}$,直线y=x-3及x轴所围成的图形的面积为( )
| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
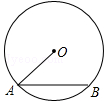
9.如图,已知⊙O的半径为5mm,弦AB=8mm,则圆心O到AB的距离是( )

| A. | 1mm | B. | 2mmm | C. | 3mm | D. | 4mm |
19.已知函数y=f(lg(x+1))的定义域为(0,99],则函数y=f[log2(x+2)]的定义域为( )
| A. | (-1,2] | B. | (-1,3) | C. | (-2,1] | D. | (-1,2) |
3.某研究机构对高二文科学生的记忆力x和判断力y进行统计分析,得下表数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出f'(x)=3x2-6x关于f'(x)=0的线性回归方程x1=0;
(3)试根据(2)求出的线性回归方程,预测记忆力为14的同学的判断力.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x.
| X | 6 | 8 | 10 | 12 |
| Y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出f'(x)=3x2-6x关于f'(x)=0的线性回归方程x1=0;
(3)试根据(2)求出的线性回归方程,预测记忆力为14的同学的判断力.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x.