题目内容
6.已知二次函数f(x)=ax2+bx+1满足f(-1)=0,且x∈R时,f(x)的值域为[0,+∞).(1)求f(x)的表达式;
(2)设函数g(x)=f(x)-2kx,k∈R.
①若g(x)在x∈[-2,2]时是单调函数,求实数k的取值范围;
②若g(x)在x∈[-2,2]上的最小值g(x)min=-15,求k值.
分析 (1)由题意可得f(-1)=0,判别式为0,解方程可得a=1,b=2,进而得到函数的解析式;
(2)①根据二次函数的性质即可求出k的范围.
②需要分类讨论,根据二次函数的性质即可求出k的值.
解答 解:(1)由题意得:$\left\{\begin{array}{l}a-b+1=0\\ \frac{{4a-{b^2}}}{4a}=0\end{array}\right.$,得$\left\{\begin{array}{l}a=1\\ b=2\end{array}\right.$,
所以f(x)=x2+2x+1,
(2)①g(x)=x2-2(k-1)x+1;
所以k-1≤-2或k-1≥2,即k≤-1或k≥3;
②当k-1≤-2即k≤-1时,g(x)min=g(-2)=4k+1=-15,得k=-4;
当k-1≥2即k≥3时,g(x)min=g(2)=9-4k=-15,得k=6;
当-2<k-1<2即-1<k<3时,$g{(x)_{min}}=g(k-1)=1-{(k-1)^2}=-15$,得k=-3(舍)或k=5(舍)
综上k=-4或k=6.
点评 本题考查函数的解析式的求法,注意运用二次函数的值域,考查函数的单调性的运用,属于中档题

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
14.在复平面内,M、N两点对应的复数分别为1-3i、-2+i,则|MN|=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | 5 |
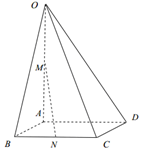 如图,在四棱锥O-ABCD中,底面ABCD是四边长为$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M为OA的中点,N为BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是四边长为$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M为OA的中点,N为BC的中点. 已知函数f(x)=-x2+2x+3,x∈[-1,2)
已知函数f(x)=-x2+2x+3,x∈[-1,2)