题目内容
19．已知函数y=f（lg（x+1））的定义域为（0，99]，则函数y=f[log2（x+2）]的定义域为（ ）| A． | （-1，2] | B． | （-1，3） | C． | （-2，1] | D． | （-1，2） |
分析 根据复合函数定义域之间的关系进行求解即可．
解答 解：∵y=f[lg（x+1）]的定义域为（0，99]，
∴0＜x≤99，
∴1＜x+1≤100，
0＜lg（x+1）≤2，
即函数f（x）的定义域为（0，2]，
由0＜log2（x+2）≤2得1＜x+2≤4，
即-1＜x≤2，
即函数y=f[log2（x+2）]的定义域是（-1，2]．
故选：A．
点评 本题主要考查了函数定义域的求解问题，根据复合函数定义域之间的关系建立不等式关系是解题的关键．
练习册系列答案
相关题目
13．“a=3”是“直线y=-ax+2与y=$\frac{a}{9}$x-5垂直”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
7．
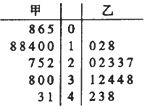从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示，设甲乙两组数据的平均数分别为x甲，x乙，中位数分别为m甲，m乙，则（ ）
从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示，设甲乙两组数据的平均数分别为x甲，x乙，中位数分别为m甲，m乙，则（ ）| A． | x甲＜x乙，m甲＞m乙 | B． | x甲＜x乙，m甲＜m乙 | C． | x甲＞x乙，m甲＞m乙 | D． | x甲＞x乙，m甲＜m乙 |
14．在复平面内，M、N两点对应的复数分别为1-3i、-2+i，则|MN|=（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{10}$ | C． | $2\sqrt{5}$ | D． | 5 |