题目内容
已知数列{an}是等差数列,且a1=2,a1+a2+a5=12.
(1)求数列{an}的通项公式;
(2)令bn=an+2n,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)令bn=an+2n,求数列{bn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知a1+a2+a5=12得到3a1+3d=12,结合首项求得公差,则等差数列的通项公式可求;
(2)把等差数列的通项公式代入bn=an+2n,分组后利用等差数列和等比数列的前n项和得答案.
(2)把等差数列的通项公式代入bn=an+2n,分组后利用等差数列和等比数列的前n项和得答案.
解答:
解:(1)由a1+a2+a5=12,得3a1+3d=12,
又a1=2,
∴d=2.
则an=2n;
(2)bn=an+2n=2n+2n,
∴Sn=(2+21)+(4+22)+…+(2n+2n)
=(2+4+…+2n)+(2+22+…+2n)
=
+
=2n+1+n2+n-2.
又a1=2,
∴d=2.
则an=2n;
(2)bn=an+2n=2n+2n,
∴Sn=(2+21)+(4+22)+…+(2n+2n)
=(2+4+…+2n)+(2+22+…+2n)
=
| n(2+2n) |
| 2 |
| 2(1-2n) |
| 1-2 |
点评:本题考查了等差数列的通项公式,考查了等差数列和等比数列的前n项和,是中档题.

练习册系列答案
相关题目
已知四面体P-ABC中,PA=4,AC=2
,PB=PC=2
,PA⊥平面PBC,则四面体P-ABC的内切球半径与外接球半径的比( )
| 7 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩B=( )
| A、(3,5] |
| B、(-1,3) |
| C、(-3,-1) |
| D、(-3,5] |
在三棱锥P-ABC中,O是底面正三角形ABC的中心,Q为棱PA上的一点,PA=1,若QO∥平面PBC,则PQ=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b∈R,t>0,下列四个条件中,使a>b成立的必要不充分条件是( )
| A、a>b-t |
| B、a>b+t |
| C、|a|>|b| |
| D、4a>4b |
函数y=lg(-x2-3x+4)的定义域是( )
| A、(-4,-1) |
| B、(-4,1) |
| C、(-1,4) |
| D、[-4,1] |
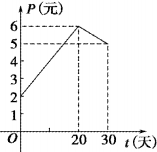 某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示: