题目内容
已知函数f(x)=ax3+bx2+cx+d(a≠0),则下列情况不可能出现的是( )
| A、f(x)有两个极值点,且极大值点大于极小值点 |
| B、f(x)有两个极值点,且极大值点小于极小值点 |
| C、f(x)有且只有一个极值点 |
| D、f(x)无极值点 |
考点:函数在某点取得极值的条件
专题:导数的综合应用
分析:求函数的导数,结合一元二次函数的性质以及函数的导数和极值之间的关系即可得到结论.
解答:
解:函数的导数f′(x)=3ax2+2bx+c,
对于二次函数的判别式△,
若△>0,函数f′(x)=3ax2+2bx+c存在两个根,此时函数f(x)存在两个极值,
若△≤0,函数f′(x)=3ax2+2bx+c为单调函数,无极值,
故f(x)有且只有一个极值点不可能出现,
故选:C
对于二次函数的判别式△,
若△>0,函数f′(x)=3ax2+2bx+c存在两个根,此时函数f(x)存在两个极值,
若△≤0,函数f′(x)=3ax2+2bx+c为单调函数,无极值,
故f(x)有且只有一个极值点不可能出现,
故选:C
点评:本题主要考查函数极值的判断,根据函数的导数以及二次函数的性质是解决本题的关键.

练习册系列答案
相关题目
已知集合A={x|-2<x<7},B={x|m+1<x<2m-1},且B≠∅,若A∪B=A,则( )
| A、-3≤m≤4 |
| B、-3<m<4 |
| C、2<m<4 |
| D、2<m≤4 |
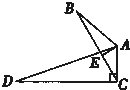
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=( )

| A、3 | ||
| B、4 | ||
C、4
| ||
| D、5 |
已知O为极点,曲线C1,C2都在极轴的上方,极坐标方程为C1:ρ=2cosθ(0≤θ≤π),C2:ρ=2(0≤θ≤π).若直线θ=α(ρ∈R,0≤α<π)与曲线C1,C2交于M,N(M不同于点O)两点,则OM2+MN2的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
设动点P(x,y)满足:
=|x+y-2|,则点P的轨迹为( )
| 2x2+2(y-2)2 |
| A、直线 | B、抛物线 |
| C、椭圆 | D、双曲线 |
设f(x)是一次函数,f(8)=15,f(2),f(5),f(14)成等比数列,令Sn=f(1)+f(2)+f(3)+…+f(n),则Sn等于( )
| A、n2 |
| B、n2-n |
| C、n2+n |
| D、以上都不对 |
已知i是虚数单位,则复数z=
所对应的点落在( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |