题目内容

解方程：3x=2-x（精确到0.1）
考点：函数的零点
专题：计算题,函数的性质及应用
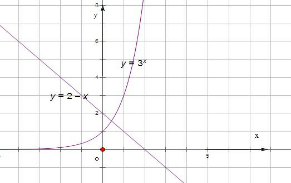
分析：先利用图象找到根所在的区间（0，1），再利用二分法把区间一次次缩小，直到满足要求为止即可．
解答： 解：由图象，知函数f（x）=3x-2+x的根x0∈（0，1）
又因为f（0）＜0，f（0.5）＞0→x0∈（0，0.5）
f（0.25）＜0，f（0.5）＞0→x0∈（0.25，0.5）
f（0.375）＜0，f（0.5）＞0→x0∈（0.375，0.5）
f（0.375）＜0，f（0.4375）＞0→x0∈（0.375，0.4375）
而0.375与0.4375精确到0.1都是0.4，所以，方程的近似解为0.4
点评：本题主要考查用二分法求区间根的问题，属于基础题型．在利用二分法求区间根的问题上，如果题中有根的精确度的限制，在解题时就一定要计算到满足要求才能结束，属于基本知识的考查．
练习册系列答案
相关题目
已知直线4x+3y-35=0与圆心在原点的圆C相切，求圆C的方程．
设A、B分别为椭圆
x2
a2
+
y2
b2
=1的左右顶点（a＞b＞0），（1，
3
2
）为椭圆上一点，椭圆的长半轴的长等于焦距．
（1）求椭圆的方程；
（2）设P（4，x），（x≠0），若直线AP，BP分别与椭圆相交于异于A、B的点M，N，求证：∠MBN为钝角．
已知函数f（x）=|x-a|．
（1）若a=1时，解不等式f（x）+f（x-1）≤4；
（2）若不等式f（x）-x＞3-2a2对x∈R恒成立，求实数a的取值范围．
已知函数f（x）=Asin（ωx+γ）（A＞0，ω＞0，|φ|＜
π
2
）的图象与y轴交与点（0，
3
），在y轴右边到y轴最近的最高点坐标为（
π
12
，2）．
（1）求f（x）；
（2）若g（x）=f（x+
π
4
），求g（x）的对称轴和对称中心．
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，0≤φ≤
π
2
）的图象在y轴右侧的第一个最高点为P（
1
3
，2），在原点右侧与x轴的第一个交点为H（
5
6
，0）
（1）求函数f（x）的解析式；
（2）求函数f（x）在区间[
1
4
，
3
4
]上的对称轴方程．
已知异面直线a，b所成的角为θ=60°，P为空间一点，则
（1）过点P与直线a，b所成的角为45°的直线有几条？
（2）过点P与直线a，b所成的角为60°的直线有几条？
（3）过点P与直线a，b所成的角为70°的直线有几条？
函数y=a|x-b|+2在（1，∞）上递增，则实数a，b满足的条件是
 
．
解方程组：
a+b=9
2
c
a
=
3
5
a2=b2+c2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网