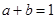题目内容
曲线 与坐标轴围成的面积是( )
与坐标轴围成的面积是( )
| A.4 | B. | C.3 | D.2 |
C
解析试题分析:根据图形的对称性,可得曲线y=cosx,x∈[0,  ]与坐标轴围成的面积等于曲线y=cosx,x∈[0,
]与坐标轴围成的面积等于曲线y=cosx,x∈[0, ]与坐标轴围成的面积的3倍,故可得结论。
]与坐标轴围成的面积的3倍,故可得结论。 ,故答案为3,选C.
,故答案为3,选C.
考点:定积分求面积
点评:本题考查定积分在求面积中的应用,解题的关键是利用余弦函数的对称性,属于基础题

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为( )
A. | B.2-ln3 | C.4+ln3 | D.4-ln3 |
设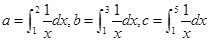 ,则下列关系式成立的是
,则下列关系式成立的是
A.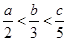 | B.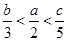 |
C.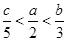 | D.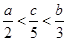 |
已知函数 有极大值和极小值,则实数
有极大值和极小值,则实数 的取值范围是( )
的取值范围是( )
A.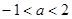 | B.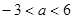 |
C.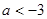 或 或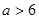 | D.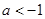 或 或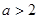 |
函数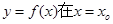 处的导数
处的导数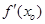 的几何意义是
的几何意义是
A.在点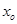 处的斜率 处的斜率 |
B.在点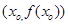 处的切线与 处的切线与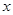 轴所夹锐角的正切值 轴所夹锐角的正切值 |
C.在点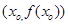 与点(0,0)连线的斜率; 与点(0,0)连线的斜率; |
D.曲线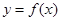 在点 在点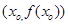 处切线的斜率 处切线的斜率 |
对于三次函数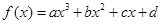 (
(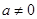 ),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数
),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数 的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数
的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数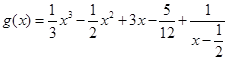 ,则
,则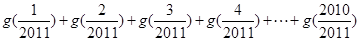 =( )
=( )
| A.2010 | B.2011 | C.2012 | D.2013 |
已知 是自然对数底数,若函数
是自然对数底数,若函数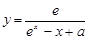 的定义域为
的定义域为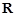 ,则实数
,则实数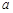 的取值范围为
的取值范围为
A.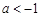 | B.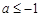 | C.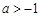 | D.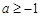 |
定义在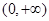 上的可导函数
上的可导函数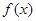 满足:
满足: 且
且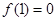 ,则
,则 的解集为( )
的解集为( )
A.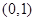 | B.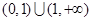 | C.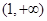 | D.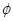 |
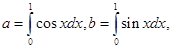 下列关系式成立的是( )
下列关系式成立的是( ) 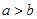 B
B 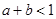 C
C  D
D