题目内容
对于三次函数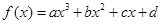 (
(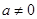 ),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数
),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数 的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数
的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数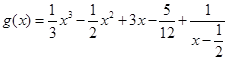 ,则
,则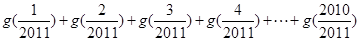 =( )
=( )
| A.2010 | B.2011 | C.2012 | D.2013 |
A
解析试题分析:因为函数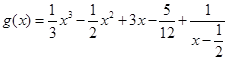 =
=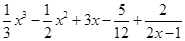 ,
,
所以令h(x)= ,m(x)=
,m(x)=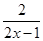 ,则g(x)=h(x)+m(x).
,则g(x)=h(x)+m(x).
则h′(x)=x2-x+3,h″(x)=2x-1,令h″(x)=0,可得x= ,故h(x)的对称中心为(
,故h(x)的对称中心为( ,1).
,1).
设点p(x0,y0)为曲线上任意一点,则点P关于( ,1)的对称点P′(1-x0,2-y0)也在曲线上,∴h(1-x0)=2-y0 ,∴h(x0)+h(1-x0)=y0+(2-y0)=2.
,1)的对称点P′(1-x0,2-y0)也在曲线上,∴h(1-x0)=2-y0 ,∴h(x0)+h(1-x0)=y0+(2-y0)=2.
所以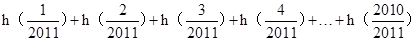
=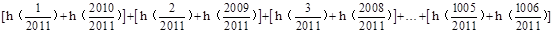 =1005×2=2010.
=1005×2=2010.
由于函数m(x)=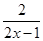 的对称中心为(
的对称中心为( ,0),可得m(x0)+m(1-x0)=0.
,0),可得m(x0)+m(1-x0)=0.
∴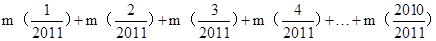
=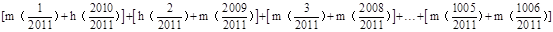 =1005×0=0.
=1005×0=0.
所以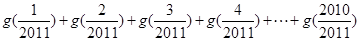 =
=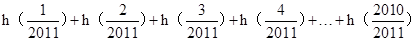 +
+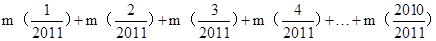
=2010+0=2010,故答案为2010.
考点:本题主要考查函数的概念,函数图象的对称性,导数的计算。
点评:难题,运用化归与转化的数学思想方法,将函数g(x)的研究进行拆分,简化了解题过程。解答此类题目,心理素质首先要过关,不畏难,静心思考。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
点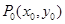 是曲线
是曲线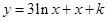
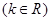 图象上一个定点,过点
图象上一个定点,过点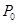 的切线方
的切线方
程为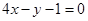 ,则实数
,则实数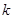 的值为( )
的值为( )
| A. 2 | B.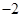 | C.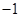 | D.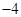 |
设动直线 与函数
与函数 的图象分别交于点
的图象分别交于点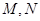 。则
。则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
曲线 与坐标轴围成的面积是( )
与坐标轴围成的面积是( )
| A.4 | B. | C.3 | D.2 |
已知函数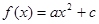 ,且
,且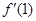 =2,则
=2,则 的值为
的值为
| A.1 | B.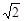 | C.-1 | D.0 |
曲线 在点P(1,12)处的切线与y轴交点的纵坐标是( )
在点P(1,12)处的切线与y轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
若曲线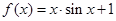 在
在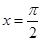 处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
| A.-2 | B.-1 | C.1 | D.2 |
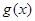 满足:①当
满足:①当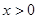 时,
时, 恒成立;②对任意的
恒成立;②对任意的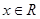 都有
都有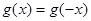 。又函数
。又函数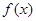 满足:对任意的
满足:对任意的 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式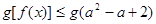 对
对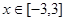 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )