题目内容
由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为( )
A. | B.2-ln3 | C.4+ln3 | D.4-ln3 |
D
解析试题分析:如图,平面图形的面积为
 dy=
dy= =4-ln3.
=4-ln3.
考点:本题考查了定积分的运用
点评:求由曲线围成的平面图形的面积,一般是应先画出它的草图,借助图形的直观性确定出被积函数以及积分的上、下限,进而由定积分求出其面积.

练习册系列答案
相关题目
函数 =
=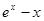 (
(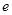
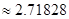 )在区间[-1,1]上的最大值是( )
)在区间[-1,1]上的最大值是( )
A.1+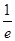 | B.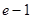 | C.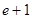 | D.1 |
若函数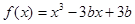 在
在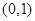 内有极小值,则 ( )
内有极小值,则 ( )
A.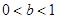 | B.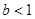 | C.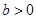 | D.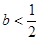 |
函数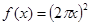 的导数是( )
的导数是( )
A.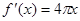 | B.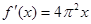 | C.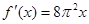 | D.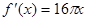 |
从如图所示的正方形OABC区域内任取一个点 ,则点M取自阴影部分的概率为
,则点M取自阴影部分的概率为 
A. | B. | C. | D. |
已知函数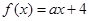 ,若
,若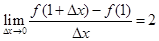 ,则实数
,则实数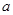 的值为( )
的值为( )
A.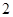 | B.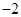 | C.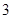 | D.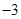 |
点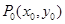 是曲线
是曲线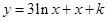
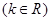 图象上一个定点,过点
图象上一个定点,过点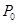 的切线方
的切线方
程为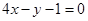 ,则实数
,则实数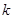 的值为( )
的值为( )
| A. 2 | B.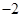 | C.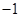 | D.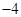 |
过点(0,1)且与曲线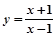 在点(3,2)处的切线垂直的直线的方程为( )
在点(3,2)处的切线垂直的直线的方程为( )
A.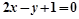 | B.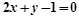 |
C.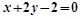 | D.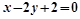 |
曲线 与坐标轴围成的面积是( )
与坐标轴围成的面积是( )
| A.4 | B. | C.3 | D.2 |