题目内容
函数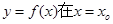 处的导数
处的导数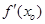 的几何意义是
的几何意义是
A.在点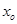 处的斜率 处的斜率 |
B.在点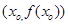 处的切线与 处的切线与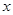 轴所夹锐角的正切值 轴所夹锐角的正切值 |
C.在点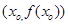 与点(0,0)连线的斜率; 与点(0,0)连线的斜率; |
D.曲线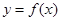 在点 在点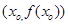 处切线的斜率 处切线的斜率 |
D
解析试题分析:结合导数的几何意义,函数在某处的导数就是某处切线的斜率,所以函数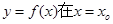 处的导数
处的导数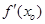 的几何意义是曲线
的几何意义是曲线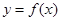 在点
在点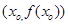 处切线的斜率。故选D。
处切线的斜率。故选D。
考点:导数的几何意义
点评:我们在求曲线的切线时,常要求出斜率,因而常用到导数。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知函数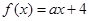 ,若
,若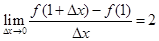 ,则实数
,则实数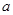 的值为( )
的值为( )
A.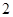 | B.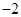 | C.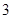 | D.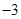 |
若函数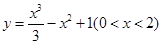 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为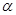 ,则
,则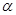 的最小值是( )
的最小值是( )
A.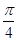 | B. | C. | D.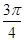 |
曲线 与坐标轴围成的面积是( )
与坐标轴围成的面积是( )
| A.4 | B. | C.3 | D.2 |
曲线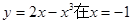 处的切线方程为( )
处的切线方程为( )
A.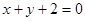 | B. |
C.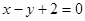 | D.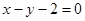 |
曲线 在点P(1,12)处的切线与y轴交点的纵坐标是( )
在点P(1,12)处的切线与y轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
已知函数 则( )
则( )
| A.无法确定 | B. |
C. | D. |
已知函数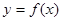 的大致图象如图所示, 则函数
的大致图象如图所示, 则函数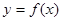 的解析式应为( )
的解析式应为( )
A. | B.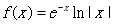 |
C. | D.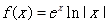 |
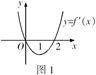
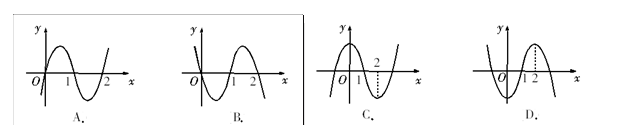
 是函数
是函数 的导函数,
的导函数, 的图象如图1所示,则
的图象如图1所示,则 的图象最有可能的是
的图象最有可能的是