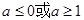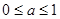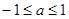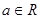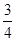题目内容
定义在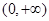 上的可导函数
上的可导函数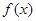 满足:
满足: 且
且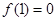 ,则
,则 的解集为( )
的解集为( )
A.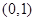 | B.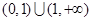 | C.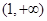 | D.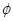 |
C
解析试题分析:令 ,则
,则 ,∵
,∵ ,∴
,∴ ,∴g(x)在
,∴g(x)在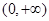 上单调递减,又
上单调递减,又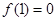 ,故g(1)=0,故
,故g(1)=0,故 等价于g(x)<g(1), ∴x>1,∴
等价于g(x)<g(1), ∴x>1,∴ 的解集为
的解集为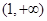
考点:本题考查了导数的运用
点评:构造函数利用导数法研究函数的单调性取求不等式的解集是解决此类问题的关键

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
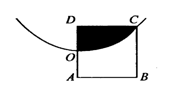
曲线 与坐标轴围成的面积是( )
与坐标轴围成的面积是( )
| A.4 | B. | C.3 | D.2 |
函数 ,已知
,已知 在
在 时取得极值,则
时取得极值,则 =
=
| A.2 | B.3 | C.4 | D.5 |
曲线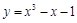 的一条切线垂直于直线
的一条切线垂直于直线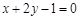 , 则切点P0的坐标为:
, 则切点P0的坐标为:
A.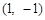 | B.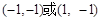 |
C.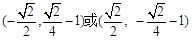 | D. |
已知函数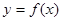 的大致图象如图所示, 则函数
的大致图象如图所示, 则函数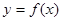 的解析式应为( )
的解析式应为( )
A. | B.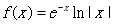 |
C. | D.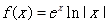 |
曲线 与直线
与直线 所围成图形的面积为( )
所围成图形的面积为( )
| A.2 | B.1 | C. | D. |
导函数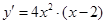 在[-2,2]上的最大值为( )
在[-2,2]上的最大值为( )
A. | B.16 | C.0 | D.5 |
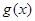 满足:①当
满足:①当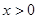 时,
时, 恒成立;②对任意的
恒成立;②对任意的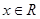 都有
都有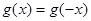 。又函数
。又函数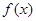 满足:对任意的
满足:对任意的 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式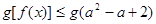 对
对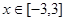 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )