题目内容
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.(Ⅰ)证明:A1C⊥平面BED.
(Ⅱ)求二面角A1-DE-B大小.
(Ⅲ)求A1D与平面BED所成角以及点A1到面BED的距离.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定,直线与平面所成的角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:分别以射线AB,AD,AA1为正方向建立空间直角坐标系O-xyz.
对第(Ⅰ)问,在平面BED内找两个不共线的向量
,
,只需
•
=0,且
•
=0即可.
对第(Ⅱ)问,先求得两半平面BED与A1ED的法向量,通过两法向量的夹角可探究二面角A1-DE-B的大小.
对第(Ⅲ)问,根据向量
,法向量
的夹角与线面角互余,可先求
与
的夹角即可达到目的;点A1到平面BED的距离可转化为向量
在平面BED的法向量方向上的射影长,从而利用向量数量积的几何意义解决.
对第(Ⅰ)问,在平面BED内找两个不共线的向量
| BE |
| DE |
| A1C |
| BE |
| A1C |
| DE |
对第(Ⅱ)问,先求得两半平面BED与A1ED的法向量,通过两法向量的夹角可探究二面角A1-DE-B的大小.
对第(Ⅲ)问,根据向量
| A1D |
| A1C |
| A1D |
| A1C |
| A1D |
解答:
解:如右图所示,分别以射线AB,AD,AA1为正方向建立空间直角坐标系O-xyz.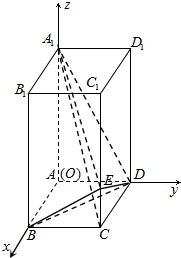
(Ⅰ)证明:根据题中数据知,A(0,0,0),B(2,0,0),C(2,2,0),
D(0,2,0),A1(0,0,4),E(2,2,1),
则
=(2,2,-4),
=(0,2,1),
=(2,0,1),
=(0,2,-4),
由
•
=2×0+2×2+(-4)×1=0知,A1C⊥BE,
同理,由
•
=2×2+2×0+(-4)×1=0知,A1C⊥DE,
又BE∩DE=E,∴A1C⊥平面BED.
(Ⅱ)由(Ⅰ)知
=(2,2,-4)是平面BED的一个法向量,
设
=(x,y,z)为平面A1ED的法向量,则由
,
得
,从而
,
取z=2,得
=(-1,4,2),
∴cos<
,
>=
=
=-
.
由图易知,两法向量
=(2,2,-4)与
=(-1,4,2)均指向二面角之外,
∴向量
,
所成的角与所求二面角互补,
从而知,所求二面角的大小为arccos
.
(Ⅲ)cos<
,
>=
=
=
.
设A1D与平面BED所成角为θ,则θ+<
,
>=
,
∴sinθ=cos<
,
>=
,得θ=arcsin
.
又设点A1到面BED的距离为h,则h=|
|sinθ=
×
=
.
故A1D与平面BED所成角为arcsin
,点A1到面BED的距离为
.

(Ⅰ)证明:根据题中数据知,A(0,0,0),B(2,0,0),C(2,2,0),
D(0,2,0),A1(0,0,4),E(2,2,1),
则
| A1C |
| BE |
| DE |
| A1D |
由
| A1C |
| BE |
同理,由
| A1C |
| DE |
又BE∩DE=E,∴A1C⊥平面BED.
(Ⅱ)由(Ⅰ)知
| A1C |
设
| n |
|
得
|
|
取z=2,得
| n |
∴cos<
| A1C |
| n |
| ||||
|
|
| 2×(-1)+2×4+(-4)×2 | ||||
|
| ||
| 42 |
由图易知,两法向量
| A1C |
| n |
∴向量
| A1C |
| n |
从而知,所求二面角的大小为arccos
| ||
| 42 |
(Ⅲ)cos<
| A1D |
| A1C |
| ||||
|
|
| (0,2,-4)•(2,2,-4) | ||||
|
| ||
| 6 |
设A1D与平面BED所成角为θ,则θ+<
| A1D |
| A1C |
| π |
| 2 |
∴sinθ=cos<
| A1D |
| A1C |
| ||
| 6 |
| ||
| 6 |
又设点A1到面BED的距离为h,则h=|
| A1D |
| 20 |
| ||
| 6 |
5
| ||
| 3 |
故A1D与平面BED所成角为arcsin
| ||
| 6 |
5
| ||
| 3 |
点评:本题考查了线面垂直的判定定理,二面角、线面角的求法及点到平面的距离的求法.根据几何体的特征,本题易于建系,故利用空间向量法求解,求解时应注意以下几点:
1.求二面角时,对于两法向量的夹角与二面角的关系,有时不易判断,常见方法是:
(1)从图观察二面角是锐角还是钝角;
(2)看两法向量的指向,若为“同进同出”,则二面角的大小与两法向量的夹角互补;若为“一出一进”,则二面角的大小与两法向量的夹角相等.
通过以上两种方法,一般可通过两法向量的余弦值得到二面角的大小
2.求线面角时,一般先求线面角的余角,因为余角可通过平面法向量与已知直线方向上的向量夹角来探求.
1.求二面角时,对于两法向量的夹角与二面角的关系,有时不易判断,常见方法是:
(1)从图观察二面角是锐角还是钝角;
(2)看两法向量的指向,若为“同进同出”,则二面角的大小与两法向量的夹角互补;若为“一出一进”,则二面角的大小与两法向量的夹角相等.
通过以上两种方法,一般可通过两法向量的余弦值得到二面角的大小
2.求线面角时,一般先求线面角的余角,因为余角可通过平面法向量与已知直线方向上的向量夹角来探求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在直线y=2x+1上有一点P,过点P且垂直于直线4x+3y-3=0的直线与圆x2+y2-2x=0有公共点,则点P的横坐标的取值范围是( )
| A、(-∞,-1)∪(1,+∞) | ||||
| B、(-1,1) | ||||
C、[-
| ||||
D、(-
|
 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取24人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取24人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为