题目内容
14.已知a-a-1=1,求a18+323a-6的值.分析 利用方程结合公式:a2+b2=(a+b)2-2ab,再用了立方和公式,提公因式,用a18+323a-6来表示.通过化简求解即可.
解答 解:∵a-a-1=1,∴a2-a-2=(a-a-1)2+2=3
=3,
a4+a-4=(a2-a-2)2-2
=7,
a8+a-8=(a4+a-4)2-2
=47,
a12+a-12=(a4+a-4)(a8+a-8-1)
=7×(47-1)
=322,
a18+323a-6
=(a18+a-6)+322a-6=a6(a12+a-12)+322a-6=322a6+322a-6=322(a6+a-6),
a6+a-6=(a2+a-2)(a4+a-4-1)
=3×(7-1)
=18.
∴a18+323a-6=322×18=5796.
点评 此题考查函数与方程的应用,在计算中要灵活运用完全平方公式和立方和公式,计算较复杂,要注意计算能力的培养.

练习册系列答案
相关题目
5.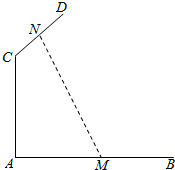 如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )
如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )
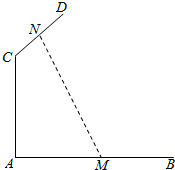 如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )
如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )| A. | 0 | B. | 3π | C. | 16π | D. | 8π |
19.“实数m=-$\frac{1}{2}$”是“直线l1:x+2my-3=0和直线l2:(3m+1)x-my-1=0相互平行”的 ( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |