题目内容
10.设tan(π+α)=2,求值:(1)$\frac{sin(α-3π)+cos(π+α)}{sin(-α)-cos(π-α)}$;
(2)3sin2α-sinαcosα+2.
分析 (1)(2)利用诱导公式、同角三角函数基本关系式、“弦化切”即可得出.
解答 解:(1)∵tan(π+α)=2,∴tanα=2.
∴$\frac{sin(α-3π)+cos(π+α)}{sin(-α)-cos(π-α)}$=$\frac{-sinα-cosα}{-sinα+cosα}$=$\frac{tanα+1}{tanα-1}$=3;
(2)3sin2α-sinαcosα+2=$\frac{3si{n}^{2}α-sinαcosα}{si{n}^{2}α+co{s}^{2}α}$+2=$\frac{3ta{n}^{2}α-tanα}{ta{n}^{2}α+1}$+2=$\frac{3×{2}^{2}-2}{{2}^{2}+1}$+2=4.
点评 本题考查了诱导公式、同角三角函数基本关系式、“弦化切”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{ax+1,x≤0}\\{lo{g}_{3}x,x>0}\end{array}\right.$,则下列关于函数y=f[f(x)]+1的零点个数是( )
| A. | 当a>0时,函数F(x)有2个零点 | B. | 当a>0时,函数F(x)有4个零点 | ||
| C. | 当a<0时,函数F(x)有2个零点 | D. | 当a<0时,函数F(x)有3个零点 |
1.直线3x+5y-7=0的斜率是( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{5}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{5}$ |
5.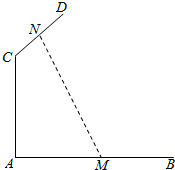 如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )
如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )
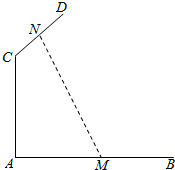 如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )
如图,AB、CD为互相垂直的两异面直线,AC⊥AB,AC⊥CD,线段AC长为2,M∈AB,N∈CD,P为MN中点,且线段MN长为4,则点P的轨迹所形成的面积为( )| A. | 0 | B. | 3π | C. | 16π | D. | 8π |
19.“实数m=-$\frac{1}{2}$”是“直线l1:x+2my-3=0和直线l2:(3m+1)x-my-1=0相互平行”的 ( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |