题目内容
给定椭圆C: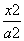 +
+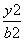 =1(a>b>0),称圆心在原点O、半径是
=1(a>b>0),称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(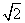 ,0),其短轴的一个端点到点F的距离为
,0),其短轴的一个端点到点F的距离为 .
.
(1) 求椭圆C和其“准圆”的方程;
(2) 若点A是椭圆C的“准圆”与x轴正半轴的交点,B、D是椭圆C上的两相异点,且BD⊥x轴,求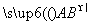 ·
· 的取值范围;
的取值范围;
(3) 在椭圆C的“准圆”上任取一点P,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,试判断l1,l2是否垂直?并说明理由.
解:(1) 由题意知c=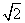 ,且a=
,且a= =
= ,可得b=1,故椭圆C的方程为
,可得b=1,故椭圆C的方程为 +y2=1,其“准圆”方程为x2+y2=4.
+y2=1,其“准圆”方程为x2+y2=4.
(2) 由题意,可设B(m,n),D(m,-n)(- <m<
<m< ),则有
),则有 +n2=1,又A点坐标为(2,0),故
+n2=1,又A点坐标为(2,0),故 =(m-2,n),
=(m-2,n), =(m-2,-n),故
=(m-2,-n),故 ·
· =(m-2)2-n2=m2-4m+4-
=(m-2)2-n2=m2-4m+4- =
= m2-4m+3=
m2-4m+3=
 ,又-
,又- <m<
<m< ,故
,故
 ∈[0,7+4
∈[0,7+4 ],所以
],所以 的取值范围是[0,7+4
的取值范围是[0,7+4 ).
).
(3) 设P(s,t),则s2+t2=4.当s=± 时,t=±1,则l1,l2其中之一斜率不存在,另一斜率为0,显然有l1⊥l2.当s≠±
时,t=±1,则l1,l2其中之一斜率不存在,另一斜率为0,显然有l1⊥l2.当s≠± 时,设过P(s,t)且与椭圆有一个公共点的直线l的斜率为k,则l的方程为y-t=k(x-s),代入椭圆C方程可得x2+3[kx+(t-ks)]2=3,即(3k2+1)x2+6k(t-ks)x+3(t-ks)2-3=0,由Δ=36k2(t-ks)2-4(3k2+1)[3(t-ks)2-3]=0,可得(3-s2)k2+2stk+1-t2=0,其中3-s2=0,设l1,l2的斜率分别为k1,k2,则k1,k2是上述方程的两个根,故k1k2=
时,设过P(s,t)且与椭圆有一个公共点的直线l的斜率为k,则l的方程为y-t=k(x-s),代入椭圆C方程可得x2+3[kx+(t-ks)]2=3,即(3k2+1)x2+6k(t-ks)x+3(t-ks)2-3=0,由Δ=36k2(t-ks)2-4(3k2+1)[3(t-ks)2-3]=0,可得(3-s2)k2+2stk+1-t2=0,其中3-s2=0,设l1,l2的斜率分别为k1,k2,则k1,k2是上述方程的两个根,故k1k2= =-1,即l1⊥l2.综上可知,对于椭圆C上的任意点P,都有l1⊥l2.
=-1,即l1⊥l2.综上可知,对于椭圆C上的任意点P,都有l1⊥l2.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 )为其终边上一点,且cosα=
)为其终边上一点,且cosα= x,求sinα的值.
x,求sinα的值.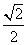 的直线l与椭圆
的直线l与椭圆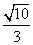 时,求k的值.
时,求k的值. ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,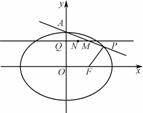

 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标.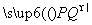 =λ
=λ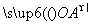 ,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
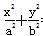 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为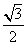 ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.