题目内容

12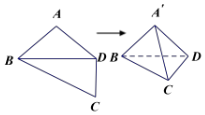．如图，在平面四边形ABCD中，AB=AD=CD=1，$BD=\sqrt{2}$，BD⊥CD，将其沿对角线BD折成四面体A′-BCD，使平面A′BD⊥平面BCD，若四面体A′-BCD顶点在同一球面上，则该球的表面积为（　　）
A．$\frac{{\sqrt{3}}}{2}π$B．3πC．$\frac{{\sqrt{2}}}{3}π$D．2π

分析 由题意，BC的中点就是球心，求出球的半径，即可得到球的表面积．

解答 解：由题意，四面体A-BCD顶点在同一个球面上，△BCD和△ABC都是直角三角形，
所以BC的中点就是球心，所以BC=$\sqrt{3}$，球的半径为：$\frac{\sqrt{3}}{2}$，
所以球的表面积为：$4π•（\frac{\sqrt{3}}{2}）^{2}$=3π．
故选B．

点评 本题是基础题，考查四面体的外接球的表面积的求法，找出外接球的球心，是解题的关键，考查计算能力，空间想象能力．

练习册系列答案
相关题目
2．执行下面的程序框图，输出的S的值为（　　）
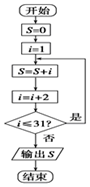
A．225B．256C．289D．324
3．直角坐标系中，点$（1，-\sqrt{3}）$的极坐标可以是（　　）
A．$（2，\frac{5π}{6}）$B．$（2，\frac{11π}{6}）$C．$（2，\frac{4π}{3}）$D．$（2，\frac{5π}{3}）$
20．某几何体的三视图如图所示，则其表面积为（　　）
A．18B．20C．22D．24
7．平面直角坐标系中，动圆C与圆（x-1）2+y2=$\frac{1}{4}$外切，且与直线x=-$\frac{1}{2}$相切，记圆心C的轨迹为曲线T
（Ⅰ）求曲线T的方程；
（Ⅱ）设过定点Q（m，0）（m为非零常数）的动直线l与曲线T交于A、B两点，问：在曲线T上是否存在点P（与A、B两点相异），当直线PA、PB的斜率存在时，直线PA、PB的斜率之和为定值，若存在，求出点P的坐标；若不存在，请说明理由．
17．将三项式（x2+x+1）n展开，当n=1，2，3，…时，得到如下所示的展开式，如图所示的广义杨辉三角形：
（x2+x+1）0=1
（x2+x+1）1=x2+x+1
（x2+x+1）2=x4+2x3+3x2+2x+1
（x2+x+1）3=x6+3x5+6x4+7x3+6x2+3x+1
观察多项式系数之间的关系，可以仿照杨辉三角形构造如图所示的广义杨辉三角形，其构造方法：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第k行共有2k+1个数．若在（a+x）（x2+x+1）4的展开式中，x6项的系数为46，则实数a的值为3．
4．一几何体由一个四棱锥和一个球组成，四棱锥的顶点都在球上，几何体的三视图如图所示，其中正视图和侧视图完全相同，球的表面积是36π，四棱锥的体积为（　　）
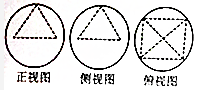
A．18B．9C．9$\sqrt{2}$D．18$\sqrt{2}$
1．已知复数z1=2t+i，z2=1-2i，若$\frac{z_1}{z_2}$为实数，则实数t的值是（　　）
A．1B．-1C．$\frac{1}{4}$D．-$\frac{1}{4}$
5．在平面直角坐标系xOy中，已知直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=6cosθ．
（Ⅰ）写出直线l的普通方程和曲线C的直角坐标方程；
（Ⅱ）若点P的直角坐标为（1，0），曲线C与直线l交于A，B两点，求|PA|+|PB|的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网