题目内容
设集合M={x|（x+3）（x-2）＜0}，N={x|1≤x≤3}，则M∪N=（ ）
| A、[1，2） |
| B、[1，2] |
| C、（-3，3] |
| D、[2，3] |
考点：并集及其运算
专题：集合
分析：利用并集定义求解．
解答：
解：∵集合M={x|（x+3）（x-2）＜0}={x|-3＜x＜2}，
N={x|1≤x≤3}，
∴M∪N={x|-3＜x≤3}=（-3，3]．
故选：C．
N={x|1≤x≤3}，
∴M∪N={x|-3＜x≤3}=（-3，3]．
故选：C．
点评：本题考查并集的求法，是基础题，解题时要认真审题．
练习册系列答案
阅读快车系列答案
相关题目
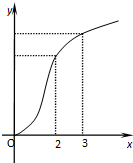已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）A、0＜f′（2）＜f′（3）＜
| ||
B、0＜f′（3）＜
| ||
C、0＜f′（3）＜f′（2）＜
| ||
D、0＜
|
记凸k边形的内角和为f（k），则f（k+1）-f（k）=（ ）
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
（文科）已知-3＜a＜-2，3＜b＜4，则
的取值范围为（ ）
| a2 |
| b |
| A、（1，3） | ||||
B、（
| ||||
C、（
| ||||
D、（
|
椭圆
+
=1的焦点坐标是（ ）
| x2 |
| 10 |
| y2 |
| 6 |
| A、（0，-4），（0，4） |
| B、（-4，0），（4，0） |
| C、（-2，0），（2，0） |
| D、（0，-2），（0，2） |
方程
-
=1表示双曲线的必要不充分条件是（ ）
| x2 |
| 2+m |
| y2 |
| m+1 |
A、（-∞，-2）∪（-
| ||
| B、（-∞，-2）∪（-1，+∞） | ||
| C、（-∞，-2） | ||
| D、（-2，-1） |