题目内容
方程
-
=1表示双曲线的必要不充分条件是( )
| x2 |
| 2+m |
| y2 |
| m+1 |
A、(-∞,-2)∪(-
| ||
| B、(-∞,-2)∪(-1,+∞) | ||
| C、(-∞,-2) | ||
| D、(-2,-1) |
考点:必要条件、充分条件与充要条件的判断,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:先求出该方程表示双曲线时的m的取值范围,再根据必要不充分条件的概念即可找出正确选项.
解答:
解:若该方程表示双曲线,则:(2+m)(m+1)>0,解得m<-2或m>-1,即m∈(-∞,-2)∪(-1,+∞);
因为找该方程表示双曲线的必要不充分条件,所以就看由该方程表示双曲线能得到哪个选项,而由该选项的m的取值范围得不到该方程表示双曲线.
∴A选项正确;
选项B应是充要条件,C应是充分不必要条件,D应是既不充分又不必要条件.
故选:A.
因为找该方程表示双曲线的必要不充分条件,所以就看由该方程表示双曲线能得到哪个选项,而由该选项的m的取值范围得不到该方程表示双曲线.
∴A选项正确;
选项B应是充要条件,C应是充分不必要条件,D应是既不充分又不必要条件.
故选:A.
点评:本题考查双曲线的标准方程,必要不充分条件的概念.

练习册系列答案
相关题目
设集合M={x|(x+3)(x-2)<0},N={x|1≤x≤3},则M∪N=( )
| A、[1,2) |
| B、[1,2] |
| C、(-3,3] |
| D、[2,3] |
复数z=
(i是虚数单位),在复平面内对应的点所在的象限( )
| 7-i |
| 3+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
从6人中选派4人承担甲,乙,丙三项工作,每项工作至少有一人承担,则不同的选派方法的个数为( )
| A、1080 | B、540 |
| C、180 | D、90 |
在如图所示的茎叶图中,甲、乙两组数据的中位数分别是.( )


| A、42,42 |
| B、45,46 |
| C、35,42 |
| D、47,48 |
如图,已知扇形AOB的圆心角为
,半径长为6,则
长为( )

| 2π |
| 3 |
 |
| AB |

| A、π | B、2π | C、3π | D、4π |
抛物线y2=ax的准线方程是x=-2,则a的值是( )
A、
| ||
B、-
| ||
| C、8 | ||
| D、-8 |
已知奇函数f(x)在[-1,0]上为单调递减函数,又α,β为锐角三角形两内角,下列结论正确的是( )
| A、f(cosα)>f(cosβ) |
| B、f(sinα)>f(sinβ) |
| C、f(sinα)>f(cosβ) |
| D、f(sinα)<f(cosβ) |
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图如图,则上班、下班时间行驶速度的中位数分别是( )
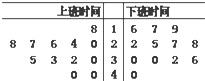

| A、28 27.5 |
| B、28 28.5 |
| C、29 27.5 |
| D、29 28.5 |