题目内容
已知以点C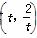 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N, 若|OM|=|ON|,求圆C的方程.
若|OM|=|ON|,求圆C的方程.
(1)证明:∵圆C过原点O,∴|OC|2=t2+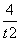 .
.
∴圆C的方程是(x-t)2+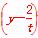 2=t2+
2=t2+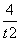 .
.
令x=0,得y1=0,y2=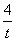 ;令y=0,得x1=0,x2=2t.
;令y=0,得x1=0,x2=2t.
∴S△OAB=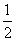 |OA|·|OB|=
|OA|·|OB|=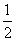 ×
× ×|2t|=4,
×|2t|=4,
即△OAB的面积为定值.
(2)解析:∵|OM|=|ON|,|CM|=|CN|,
∴OC垂直平分线段MN.
∵kMN=-2,∴kOC=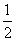 .∴直线OC的方程是y=
.∴直线OC的方程是y=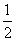 x.
x.
∴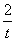 =
=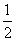 t,解得t=2或t=-2.
t,解得t=2或t=-2.
当t=2时,圆心C的坐标 为(2,1),|OC|=
为(2,1),|OC|=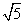 ,此时C到直线y=-2x+4的距离d=
,此时C到直线y=-2x+4的距离d=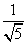 <
<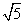 ,满足圆C与直线y=-2x+4相交于两点.
,满足圆C与直线y=-2x+4相交于两点.
当t=-2时,圆心C的坐标为(-2,-1),|OC|=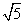 ,此时C到直线y=-2x+4的距离d=
,此时C到直线y=-2x+4的距离d=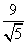 >
>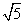 .此时圆C与直线y=-2x+4不相交,
.此时圆C与直线y=-2x+4不相交,
∴t=-2不符合题意,舍去.
∴圆C的方程为(x-2)2+(y-1)2=5.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
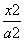 +
+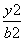 =1(a>b
=1(a>b >0)的左焦点为F,离心率
>0)的左焦点为F,离心率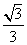 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为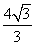 .
.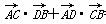 =8,求k的值.
=8,求k的值.
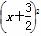 +y2=
+y2=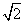 ,则直线l的斜率为____________.
,则直线l的斜率为____________.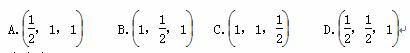
 平面ABCD和平面ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
平面ABCD和平面ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<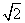 ).
).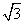 y=0截圆(x-2)2+y2=4所得劣弧所对的圆心角是( )
y=0截圆(x-2)2+y2=4所得劣弧所对的圆心角是( )