题目内容
正方形ABCD、ABEF的边长都是1，而且
平面ABCD和平面ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM＝BN＝a(0＜a＜
)．
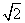(1)求MN的长；
(2)a为何值时，MN的长最小？
解析：(1)因为平面ABCD⊥平面ABEF，
平面ABCD∩平面ABEF＝AB，AB⊥BE，
所以BE⊥平面ABCD，则AB，BE，BC两两垂直，
以B为坐标原点，以BA，BE，BC分别为x，y，z轴建立空间直角坐标系(图略)，
则
|MN|＝
＝
(2)由(1)知，当a＝
时， |MN|最短，为.
此时M，N恰好为AC，BF的中点．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
x＋b的图象关于直线y＝x对称，则a＋b＝____________.
.记动点P的轨迹为W.
的最小值．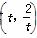
(t∈R，t≠0)为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．
若|OM|＝|ON|，求圆C的方程．
y2＝x的焦点，A，B是该抛物线上的两点，|AF|＋|BF|＝3，则线段AB的中点到y轴的距离为( )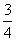
B．1 C.
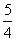D.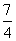
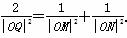请将n表示为m的函数．