题目内容
已知双曲线的方程是16x2－9y2＝144.
(1)求双曲线的焦点坐标、离心率和渐近线方程；
(2)设F1和F2是双曲线的左、右焦点，点P在双曲线上，且|PF1|·|PF2|＝32，求∠F1PF2的大小．
解析：(1)由16x2－9y2＝144，得
－
＝1，∴a＝3，b＝4，c＝5.焦点坐标为F1(－5,0)，F2(5,0)，离心率为e＝
，渐近线方程为y＝±
x.
(2)||PF1|－|PF2||＝6，
cos∠F1PF2
＝
＝
＝0.
∴∠F1PF2＝90°.
练习册系列答案
相关题目
称，直线MP，NP分别交x轴于点E(xE,0)和点F(xF,0)．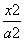
＋
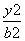＝1(a>b>0)时，探究xE·xF的值是否与点M，N，P的位置相关；
结论，无须证明)．
.
，使得m[f(x)＋
]＋2＝0恒成立，求实数m的取值范围.
中项，则圆锥曲线x2＋
＝1的离心率为( )
B.
C.
D.
．－1或3
x＋b的图象关于直线y＝x对称，则a＋b＝____________.
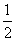x2上横坐标大于零的一点，直线l过点P并与抛物线C在点P处的切线垂直，直线l与抛物线C相交于另一点Q.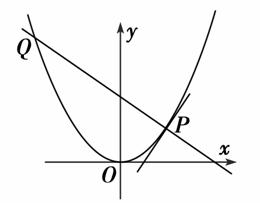
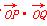＝0，求过点P，Q，O的圆的方程．
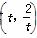(t∈R，t≠0)为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．
若|OM|＝|ON|，求圆C的方程．