题目内容
某市高三数学抽样考试中，对90分以上（含90分） 的成绩进行统计，其频率分布图如图2所示，已知130～140分数段的人数为90，90～100分数段的人数为a，则图1所示程序框图的运算结果为（注：n！=1×2×3×…×n，如5！=1×2×3×4×5）（ ）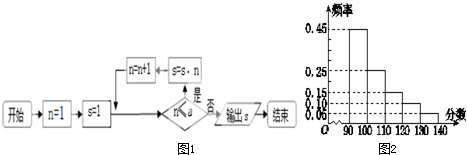
| A、800! | B、810! |
| C、811! | D、812! |
考点：程序框图,频率分布直方图
专题：算法和程序框图
分析：利用在频率分布直方图中频率=
求得a值，根据框图的流程判断算法的功能及跳出循环体的n值，可得输出S的值．
| 频数 |
| 样本容量 |
解答：
解：由频率分布直方图知：130～140分数段的频率=0.05，又频数为90，∴样本容量为
=1800，
90～100分数段的频率为0.45，∴90～100分数段的人数为a=1800×0.45=810，
根据框图的流程知：算法的功能是求S=n！的值，
∵跳出循环体的n值为811，∴输出S=810！．
故选B．
| 90 |
| 0.05 |
90～100分数段的频率为0.45，∴90～100分数段的人数为a=1800×0.45=810，
根据框图的流程知：算法的功能是求S=n！的值，
∵跳出循环体的n值为811，∴输出S=810！．
故选B．
点评：本题考查了循环结构的程序框图，考查了频率分布直方图，根据框图的流程判断跳出循环体的n值是关键．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
已知某几何体的三视图如图所示，其中侧视图为圆形，则该几何体的体积是（ ）
| A、π | B、2π | C、3π | D、6π |
在等差数列{an}中，a1=1，a3=5，则a5=（ ）
| A、3 | B、5 | C、7 | D、9 |
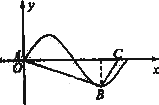已知函数f（x）=sinωx（ω＞0）的一段图象如图所示，△ABC的顶点A与坐标原点O重合，B是f（x）的图象上一个最低点，C在x轴上，若内角A，B，C所对边长为a，b，c，且△ABC的面积S满足12S=b2+c2-a2，将f（x）右移一个单位得到g（x），则g（x）的表达式为（ ）A、g（x）=cos（
| ||||
B、g（x）=-cos（
| ||||
C、g（x）=sin（
| ||||
D、g（x）=sin（
|
已知f（3x）=x•log23，则f（2）+f（4）+f（8）+…+f（28）=（ ）
| A、18 | B、36 | C、72 | D、144 |
| 5 |
| 2-i |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
若a，b，c∈C（C为复数集），则（a-b）2+（b-c）2=0是a=b=c的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |