题目内容
复数（1-i）2+（a-i）2是纯虚数，则实数a等于（ ）
| A、-1 | B、1 | C、±1 | D、0 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：利用复数的运算法则和复数定义求解．
解答：
解：（1-i）2+（a-i）2
=1-2i+i2+a2-2ai+i2
=a2-1-（2+2a）i，
∵数（1-i）2+（a-i）2是纯虚数，
∴
，解得a=1．
故选：B．
=1-2i+i2+a2-2ai+i2
=a2-1-（2+2a）i，
∵数（1-i）2+（a-i）2是纯虚数，
∴
|
故选：B．
点评：本题考是查实数的求法，是基础题，解题时要认真审题，注意复数运算法则的合理运用．
练习册系列答案
相关题目
函数y=xln|x|的大致图象是（ ）
A、 |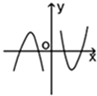
B、 |
C、 |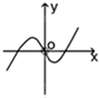
D、 |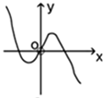
关于函数f（x）=sin（2x+
）的四个命题：
①f（x）的图象关于直线x=
对称；
②f（x）的图象关于点（
，0）对称；
③f（x）的最小正周期为π；
④f（x）在[0，
]，上为增函数，其中正确的是命题是（ ）
| π |
| 3 |
①f（x）的图象关于直线x=
| π |
| 12 |
②f（x）的图象关于点（
| π |
| 4 |
③f（x）的最小正周期为π；
④f（x）在[0，
| π |
| 2 |
| A、②③ | B、①② | C、②④ | D、①③ |
若x是纯虚数，y是实数，且2x-1+i=y-（3-y）i，则x+y等于（ ）
A、1+
| ||
B、-1+
| ||
C、1-
| ||
D、-1-
|
已知偶函数f（x）的定义域为R，则下列函数中为奇函数的是（ ）
| A、sin[f（x）] |
| B、x•f（sinx） |
| C、f（x）•f（sinx） |
| D、[f（sinx）]2 |
已知整数的数对列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），…则第60个数对是（ ）
| A、（3，8） |
| B、（4，7） |
| C、（4，8） |
| D、（5，7） |
在△ABC中，角A、B、C所对的边分别为a，b，c，且a＞b，则正确的是（ ）
| A、sinA＞sinB且cosA＞cosB |
| B、sinA＜sinB且cosA＜cosB |
| C、sinA＞sinB且cosA＜cosB |
| D、sinA＜sinB且cosA＞cosB |
一个直径为8cm的大金属球，熔化后铸成若干个直径为2cm的小球，如果不计损耗，可铸成小球的个数为（ ）
| A、4 | B、8 | C、16 | D、64 |