题目内容
从1,2,3,4,5,6这六个数中,不放回地任意取两个数,每次取一个数,则所取的两个数都是偶数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:根据已知中从1,2,3,4,5,6这6个数中,不放回地任意取两个数,我们列出所有的基本事件个数,及满足条件两个数都是偶数的基本事件个数,代入古典概型概率公式,即可得到答案.
解答:
解:从1,2,3,4这4个数中,不放回地任意取两个数,共有
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5)共30种
其中满足条件两个数都是偶数的有(2,4),(2,6),(4,2),(4,6),(6,2),(6,4)共6种情况
故从1,2,3,4,5,6这六个数中,不放回地任意取两个数,每次取一个数,则所取的两个数都是偶数的概率为P=
=
故选:D.
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5)共30种
其中满足条件两个数都是偶数的有(2,4),(2,6),(4,2),(4,6),(6,2),(6,4)共6种情况
故从1,2,3,4,5,6这六个数中,不放回地任意取两个数,每次取一个数,则所取的两个数都是偶数的概率为P=
| 6 |
| 30 |
| 1 |
| 5 |
故选:D.
点评:本题考查的知识点是古典概型公式,古典概型问题的处理方法是:计算出基本事件总数N,则满足条件A的基本事件总数A(N),代入P=A(N)÷N求了答案.

练习册系列答案
相关题目
函数y=xln|x|的大致图象是( )
A、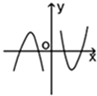 |
B、 |
C、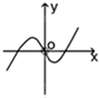 |
D、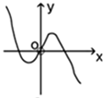 |
已知直线l1:4x-3y+11=0和直线l2:x+1=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
关于函数f(x)=sin(2x+
)的四个命题:
①f(x)的图象关于直线x=
对称;
②f(x)的图象关于点(
,0)对称;
③f(x)的最小正周期为π;
④f(x)在[0,
],上为增函数,其中正确的是命题是( )
| π |
| 3 |
①f(x)的图象关于直线x=
| π |
| 12 |
②f(x)的图象关于点(
| π |
| 4 |
③f(x)的最小正周期为π;
④f(x)在[0,
| π |
| 2 |
| A、②③ | B、①② | C、②④ | D、①③ |
若x是纯虚数,y是实数,且2x-1+i=y-(3-y)i,则x+y等于( )
A、1+
| ||
B、-1+
| ||
C、1-
| ||
D、-1-
|
已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第60个数对是( )
| A、(3,8) |
| B、(4,7) |
| C、(4,8) |
| D、(5,7) |
不等式组
的整数解的个数是( )
|
| A、2 | B、4 | C、5 | D、7 |