题目内容
7.$|{\vec a}|=\sqrt{2}$,$\vec b=(-1,1),\vec c=(2,-2),\vec a•(\vec b+\vec c)=1.\vec a与\vec b的夹角为$$\frac{2π}{3}$.分析 根据向量的坐标运算和的向量的共线定理以及向量的夹角公式计算即可.
解答 解:∵$\overrightarrow{b}$=(-1,1),$\overrightarrow{c}$=(2,-2),
∴$\overrightarrow{b}$+$\overrightarrow{c}$=(1,-1)=-$\overrightarrow{b}$,
∴|$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{2}$
设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则$\overrightarrow{a}$与$\overrightarrow{b}$+$\overrightarrow{c}$的夹角为π-θ,
∵$\overrightarrow{a}$•($\overrightarrow{b}$+$\overrightarrow{c}$)=|$\overrightarrow{a}$|•|$\overrightarrow{b}$+$\overrightarrow{c}$|cos(π-θ)=$\sqrt{2}$×$\sqrt{2}$×(-cosθ)=1,
∴coθ=-$\frac{1}{2}$,
∵0≤θ≤π,
∴θ=$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$
点评 本题考查了向量的坐标运算和的向量的共线定理以及向量的夹角公式,属于基础题

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
12.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,-1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
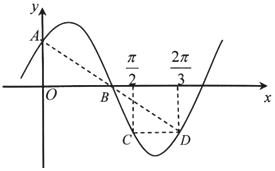 如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.
如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.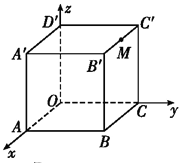 如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).
如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).