题目内容
19.在△ABC中,已知AB=4,AC=7,BC边的中线$AD=\frac{7}{2}$,那么$\overrightarrow{AB}•\overrightarrow{AC}$=-8.分析 由平行四边形法则可知2$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{AC}$,两边平方即可求出$\overrightarrow{AB}•\overrightarrow{AC}$.
解答 解:∵AD是BC边的中线,
∴2$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{AC}$,
∴($\overrightarrow{AB}+\overrightarrow{AC}$)2=(2$\overrightarrow{AD}$)2,
即${\overrightarrow{AB}}^{2}$+${\overrightarrow{AC}}^{2}$+2$\overrightarrow{AB}•\overrightarrow{AC}$=4${\overrightarrow{AD}}^{2}$,
∴16+49+2$\overrightarrow{AB}•\overrightarrow{AC}$=49,
解得$\overrightarrow{AB}•\overrightarrow{AC}$=-8.
故答案为:-8.
点评 本题考查了平面向量的数量积运算,属于中档题.

练习册系列答案
相关题目
9.某城市理论预测2000年到2004年人口总数与年份的关系如表所示
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)此次估计2005年该城市人口总数.
(参考公式:用最小二乘法求线性回归方程系数的公式:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(2)此次估计2005年该城市人口总数.
(参考公式:用最小二乘法求线性回归方程系数的公式:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
14.在等差数列{an}中,a3=3,d=2,则a1=( )
| A. | 1 | B. | -1 | C. | 7 | D. | 2 |
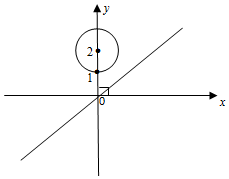 已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线上,过点P作圆M的切线PA,PB,切点为A,B.
已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线上,过点P作圆M的切线PA,PB,切点为A,B.