题目内容
14.已知复数z在复平面内对应的点为(-1,1),则复数$\frac{z+3}{z+2}$的模为( )| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 由复数z在复平面内对应的点为(-1,1),得z=-1+i,把z代入复数$\frac{z+3}{z+2}$,再利用复数代数形式的乘除运算化简,然后由复数求模公式计算得答案.
解答 解:由复数z在复平面内对应的点为(-1,1),
得z=-1+i.
则$\frac{z+3}{z+2}$=$\frac{-1+i+3}{-1+i+2}=\frac{2+i}{1+i}=\frac{(2+i)(1-i)}{(1+i)(1-i)}=\frac{3-i}{2}$=$\frac{3}{2}-\frac{1}{2}i$,
∴复数$\frac{z+3}{z+2}$的模为:$\sqrt{(\frac{3}{2})^{2}+(-\frac{1}{2})^{2}}=\frac{\sqrt{10}}{2}$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
9.已知斜率为3的直线l与双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)交于A,B两点,若点P(6,2)是AB的中点,则双曲线C的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{2}$ |
10.已知函数f(x)=ln$\frac{x}{2}$+$\frac{1}{2}$,g(x)=ex-2,对于?m∈R,?n∈(0,+∞)使得f(m)=g(n)成立,则n-m的最大值为( )
| A. | -ln2 | B. | ln2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
2.若函数f(x)=($\frac{1}{3}$)|x|-a-1有零点,则a的取值范围是( )
| A. | -1<a≤0 | B. | -1<a<0 | C. | a>-1 | D. | 0<a≤1 |
9.阅读程序框图(如图),如果输出的函数值在[1,3]上,则输入的实数x取值范围是( )
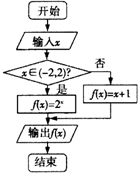

| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
6.某射击运动员进行打靶练习,已知打十枪每发的靶数为9,10,7,8,10,10,6,8,9,7,设其平均数为a,中位数为b,众数为c,则有( )
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |
3.复数z满足(1-i)z=m+i (m∈R,i为虚数单位),在复平面上z对应的点不可能在 ( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.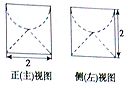 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此时几何体的体积是( )| A. | 2π | B. | $\frac{4π}{3}$ | C. | π | D. | $\frac{π}{2}$ |