题目内容
2.若函数f(x)=($\frac{1}{3}$)|x|-a-1有零点,则a的取值范围是( )| A. | -1<a≤0 | B. | -1<a<0 | C. | a>-1 | D. | 0<a≤1 |
分析 问题转化为函数的图象的交点问题,画出函数的图象,根据图象求出a的范围即可.
解答 解:若函数f(x)=($\frac{1}{3}$)|x|-a-1有零点,
则g(x)=3-|x|和y=a+1有交点,
画出函数图象,如图示:
结合图象:0<a+1≤1,解得:-1<a≤0,
故选:A.
点评 本题考查了函数的零点问题,考查数形结合思想以及转化思想,是一道中档题.

练习册系列答案
相关题目
15.函数f(x)=x-2cosx在区间$[-\frac{π}{2},0]$上的最小值是( )
| A. | $-\frac{π}{2}$ | B. | -2 | C. | $-\frac{π}{3}-1$ | D. | $-\frac{π}{6}-\sqrt{3}$ |
7.“a=2”是“函数f(x)=(x-a)2在区间[2,+∞)上为增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知复数z在复平面内对应的点为(-1,1),则复数$\frac{z+3}{z+2}$的模为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.在△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且4S=(a+b)2-c2,则sin($\frac{π}{4}$+C)等于( )
| A. | 1 | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
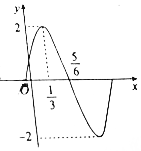 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于函数f(x)的性质的结论正确的有①②③④(填序号)