题目内容
9.已知斜率为3的直线l与双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)交于A,B两点,若点P(6,2)是AB的中点,则双曲线C的离心率等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{2}$ |
分析 设A(x1,y1),B(x2,y2),根据AB的中点P的坐标,表示出斜率,从而得到关于a、b的关系式,再求离心率.
解答 解:设A(x1,y1),B(x2,y2),
则代入双曲线方程,相减可得-$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{{a}^{2}}=\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{{b}^{2}}$,
∵点P(6,2)是AB的中点,
∴x1+x2=12,y1+y2=4,
∵直线l的斜率为3,∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=3,
∴a2=b2,c2=2a2,
∴e=$\sqrt{2}$.
故选A.
点评 本题考查了双曲线的简单性质,解题的关键是利用“设而不求”法求直线l的斜率.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1(a>0)的离心率为2,则a等于( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
14.已知复数z在复平面内对应的点为(-1,1),则复数$\frac{z+3}{z+2}$的模为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
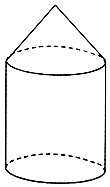 如图,某粮仓是由圆柱和圆锥构成(粮仓的底部位于地面上),圆柱的底面直径与高都等于h米,圆锥的高为$\frac{1}{2}$h米.
如图,某粮仓是由圆柱和圆锥构成(粮仓的底部位于地面上),圆柱的底面直径与高都等于h米,圆锥的高为$\frac{1}{2}$h米.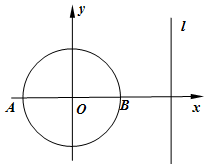 如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.
如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.