题目内容
19．已知集合A={x|$\frac{1}{4}$≤2x≤128}，B={y|y=log2x，x∈[$\frac{1}{8}$，32]}，（1）求A∩B；A∪B，
（2）若D={x|x＞6m+1}，且（A∪B）∩D=∅，求实数m的取值范围．
分析 （1）分别求出集合A和B，由此能求出A∩B，A∪B．
（2）由D={x|x＞6m+1}，A∪B={x|-3≤x≤7}，（A∪B）∩D=∅，能求出实数m的取值范围．
解答 解：（1）∵集合A={x|$\frac{1}{4}$≤2x≤128}={x|-2≤x≤7}，
B={y|y=log2x，x∈[$\frac{1}{8}$，32]}={y|-3≤y≤5]，
∴A∩B={x|-2≤x≤5}，A∪B={x|-3≤x≤7}．
（2）∵D={x|x＞6m+1}，A∪B={x|-3≤x≤7}，
（A∪B）∩D=∅，
∴6m+1≥7，解得m≥1．
∴实数m的取值范围是[1，+∞）．
点评 本题考查交集、并集的求法及应用，是基础题，解题时要认真审题，注意交集和并集性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
14．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1（a＞0）的离心率为2，则a等于（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | $\frac{3}{2}$ | D． | 1 |
15．函数f（x）=x-2cosx在区间$[-\frac{π}{2}，0]$上的最小值是（ ）
| A． | $-\frac{π}{2}$ | B． | -2 | C． | $-\frac{π}{3}-1$ | D． | $-\frac{π}{6}-\sqrt{3}$ |
7．“a=2”是“函数f（x）=（x-a）2在区间[2，+∞）上为增函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
14．已知复数z在复平面内对应的点为（-1，1），则复数$\frac{z+3}{z+2}$的模为（ ）
| A． | $\sqrt{10}$ | B． | $\frac{\sqrt{10}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
4．已知向量$\overrightarrow{a}$=（0，1），$\overrightarrow{b}$=（2，-1），则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{5}$ | C． | 2 | D． | 4 |
11．在△ABC中，三个内角A，B，C的对边分别为a，b，c，若△ABC的面积为S，且4S=（a+b）2-c2，则sin（$\frac{π}{4}$+C）等于（ ）
| A． | 1 | B． | -$\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
8．
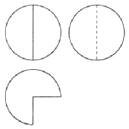如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（ ）
如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（ ）| A． | 8π | B． | $\frac{16π}{3}$ | C． | 4π | D． | $\frac{4π}{3}$ |
9．要得到函数f（x）=sin2x+$\sqrt{3}$cos2x的图象，可将y=2sin2x的图象向左平移多少个单位（ ）
| A． | $\frac{π}{6}$个 | B． | $\frac{π}{3}$个 | C． | $\frac{π}{4}$个 | D． | $\frac{π}{12}$个 |