题目内容
19.已知函数f(x)=log2||x|-1|.(1)作出函数f(x)的大致图象;
(2)指出函数f(x)的奇偶性、单调区间及零点.
分析 (1)求出函数的定义域,化简函数的解析式,然后作出函数f(x)的大致图象;
(2)利用函数的图象,指出函数f(x)的奇偶性、单调区间及零点.
解答 解:函数f(x)=log2||x|-1|的定义域为:{x|x≠±1,x∈R}.
函数f(x)=log2||x|-1|=$\left\{\begin{array}{l}{lo{g}_{2}(x-1),x>1}\\{lo{g}_{2}(1-x),0<x<1}\\{lo{g}_{2}(x+1),-1<x<0}\\{lo{g}_{2}(-x-1),x<-1}\end{array}\right.$,x=0时f(x)=0,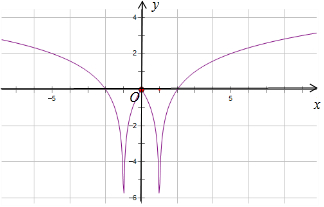
函数的图象如图:
(2)函数是偶函数,单调增区间(-1,0),(1,+∞);单调减区间为:(-∞,-1),(0,1);
零点为:0,-2,2.
点评 本题考查函数的图象的画法,函数的奇偶性以及函数的单调性零点的求法,考查计算能力.

练习册系列答案
相关题目
9.设集合A={-1,1},集合B={x|ax=1,a∈R},则使得B⊆A的a的所有取值构成的集合是( )
| A. | {0,1} | B. | {0,-1} | C. | {1,-1} | D. | {-1,0,1} |
14.设x,y∈R,a>1,b>1,若ax=by=3,a+b=6,则$\frac{1}{x}$+$\frac{1}{y}$的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |