题目内容
9.设集合A={x|x2-3x-4≤0},B={x||x|≤3},则集合A∩B=( )| A. | [-3,-1] | B. | [-3,4] | C. | [-1,3] | D. | [3,4] |
分析 根据题意,解x2-3x-4≤0可得集合A,解|x|≤3可得集合B,进而由交集的定义计算可得答案.
解答 解:根据题意,x2-3x-4≤0⇒-1≤x≤4,
即A={x|x2-3x-4≤0}={x|-1≤x≤4}=[-1,4],
|x|≤3⇒-3≤x≤3,
即B={x||x|≤3}={x|-3≤x≤3}=[-3,3],
则A∩B=[-1,3],
故选:C.
点评 本题考查集合的交集运算,关键是掌握集合的交集的定义.

练习册系列答案
相关题目
17.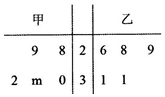 为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(位:℃)制成如图所示的茎叶图,已知甲地该月11时的平均气温比乙地该月11时的平均气温高1℃,则甲地该月11时的平均气温的标准差为( )
为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(位:℃)制成如图所示的茎叶图,已知甲地该月11时的平均气温比乙地该月11时的平均气温高1℃,则甲地该月11时的平均气温的标准差为( )
 为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(位:℃)制成如图所示的茎叶图,已知甲地该月11时的平均气温比乙地该月11时的平均气温高1℃,则甲地该月11时的平均气温的标准差为( )
为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(位:℃)制成如图所示的茎叶图,已知甲地该月11时的平均气温比乙地该月11时的平均气温高1℃,则甲地该月11时的平均气温的标准差为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
4.已知R为实数集,集合A={x|x2-2x≥0},B={x|x>1},则(∁RA)∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
1.已知向量$\overrightarrow{m}$=(-1,2),$\overrightarrow{n}$=(1,λ),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则$\overrightarrow{m}$+2$\overrightarrow{n}$与$\overrightarrow{m}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
19.若双曲线E:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F(3,0),过F点的直线l与双曲线E交于A,B两点,且AB的中点为P(-3,-6),则E的方程为( )
| A. | $\frac{{x}^{2}}{5}$$-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{6}$$-\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{6}$=1 |
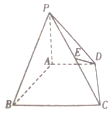 如图,在底面为直角梯形的四棱锥P-ABCD中,E为PC的中点,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=2,AD=2,AB=2$\sqrt{3}$,BC=4.
如图,在底面为直角梯形的四棱锥P-ABCD中,E为PC的中点,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=2,AD=2,AB=2$\sqrt{3}$,BC=4.