题目内容
已知点A(-1,0)、B(1,0),动点P满足:∠APB=2θ,且|PA|•|PB|cos2θ=1.(P不在线段AB上)
(1)求动点P的轨迹C的方程;
(2)过椭圆的上顶点作互相垂直的两条直线分别交椭圆于另外一点P、Q,试问直线PQ是否经过定点,若是,求出定点坐标;若不是,说明理由.
(1)求动点P的轨迹C的方程;
(2)过椭圆的上顶点作互相垂直的两条直线分别交椭圆于另外一点P、Q,试问直线PQ是否经过定点,若是,求出定点坐标;若不是,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)讨论点P在x轴上且在线段AB外时,求出点P,点P不在x轴上时,求出点P的轨迹,
从而得出点P的轨迹C的方程;
(2)设出直线AP的方程y=kx+1,代入椭圆方程,求出点P的坐标,
再求出点Q的坐标,得直线PQ的方程,判断PQ是否过定点即可.
从而得出点P的轨迹C的方程;
(2)设出直线AP的方程y=kx+1,代入椭圆方程,求出点P的坐标,
再求出点Q的坐标,得直线PQ的方程,判断PQ是否过定点即可.
解答:
解:(1)①当点P在x轴上且在线段AB外时,θ=0,设P(p,0),
由|PA|•|PB|cos2θ=1,得(p+1)(p-1)=1,
∴p=±
∴P(±
,0);…(3分)
②当点P不在x轴上时,
在△PAB中,由余弦定理得|AB|2=|PA|2+|PB|2-2|PA|•|PB|cos2θ,
∴4=(|PA|+|PB|)2-2|PA|•|PB|(1+cos2θ)
=(|PA|+|PB|)2-4|PA|•|PB|cos2θ
=(|PA|+|PB|)2-4;
∴|PA|+|PB|=2
>2=|AB|,即动点P在以A、B为两焦点的椭圆上,
方程为:
+y2=1(x≠±
);
综和①②可知:动点P的轨迹C的方程为:
+y2=1;…(6分)
(2)显然,两直线斜率存在,设AP:y=kx+1,
代入椭圆方程,得(1+2k2)x2+4kx=0,…(8分)
解得点P(
,
),
同理得Q(
,
),
直线PQ:y-
=
(x-
),…(10分)
化简得y=
x-
;
令x=0,得y=-
,
∴直线PQ过定点(0,-
)…(12分)
由|PA|•|PB|cos2θ=1,得(p+1)(p-1)=1,
∴p=±
| 2 |
| 2 |
②当点P不在x轴上时,
在△PAB中,由余弦定理得|AB|2=|PA|2+|PB|2-2|PA|•|PB|cos2θ,
∴4=(|PA|+|PB|)2-2|PA|•|PB|(1+cos2θ)
=(|PA|+|PB|)2-4|PA|•|PB|cos2θ
=(|PA|+|PB|)2-4;
∴|PA|+|PB|=2
| 2 |
方程为:
| x2 |
| 2 |
| 2 |
综和①②可知:动点P的轨迹C的方程为:
| x2 |
| 2 |
(2)显然,两直线斜率存在,设AP:y=kx+1,
代入椭圆方程,得(1+2k2)x2+4kx=0,…(8分)
解得点P(
| -4k |
| 1+2k2 |
| 1-2k2 |
| 1+2k2 |
同理得Q(
| 4k |
| 2+k2 |
| k2-2 |
| 2+k2 |
直线PQ:y-
| k2-2 |
| 2+k2 |
| k2-1 |
| 3k |
| 4k |
| 2+k2 |
化简得y=
| k2-1 |
| 3k |
| 1 |
| 3 |
令x=0,得y=-
| 2 |
| 3 |
∴直线PQ过定点(0,-
| 1 |
| 3 |
点评:本题考查了求点的轨迹的问题,也考查了直线与圆锥曲线的综合应用问题,是中档题目.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
边长分别为1,
,2
的三角形的最大角与最小角的和是( )
| 5 |
| 2 |
| A、90° | B、120° |
| C、135° | D、150° |
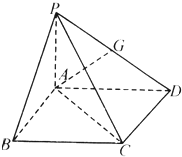 如图,在四棱锥P-ABCD中,PA⊥平面ABCD四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点.