题目内容
利用三角函数线,写出满足下列条件的角α的集合:
(1)sinα≥
;
(2)cosα≤
;
(2)|cosα|>|sinα|.
(1)sinα≥
| ||
| 2 |
(2)cosα≤
| 1 |
| 2 |
(2)|cosα|>|sinα|.
考点:三角函数线
专题:数形结合,三角函数的求值
分析:在单位圆中画出三角函数线.
(1)由[0,2π)内,sin
=sin
=
,结合正弦线得sinα≥
的解集;
(2)由[0,2π)内,cos
=cos
=
,结合余弦线得cosα≤
的解集.
(3)由[0,2π)内,|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|sin
|=
,结合余弦线、正弦线得|cosα|>|sinα|的解集.
(1)由[0,2π)内,sin
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| ||
| 2 |
(2)由[0,2π)内,cos
| π |
| 3 |
| 5π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由[0,2π)内,|sin
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
| 7π |
| 4 |
| 7π |
| 4 |
| ||
| 2 |
解答:
解:在单位圆内作三角函数线如图:
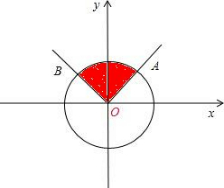
(1)∵在[0,2π)内,sin
=sin
=
,
OA,OB分别为
,
的终边,由正弦线可知,
满足sinα≥
的角的终边在劣弧AB内,
∴sinα≥
的解集为{α|
+2kπ≤α≤
+2kπ,k∈Z};
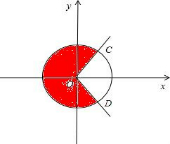
(2)∵在[0,2π)内,cos
=cos
=
,
OC,OD分别为
,
的终边,由余弦线可知,
满足cosα≤
的终边在劣弧CD内,
∴cosα≤
的解集为{α|
+2kπ≤α≤
+2kπ,k∈Z}.
(3)∵在[0,2π)内,|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|sin
|=
,
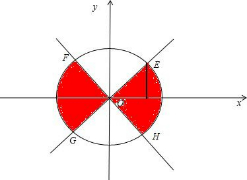
OE,OF,OG,OH分别为
,
,
,
的终边,由余弦线可知,
满足cosα≤
的终边在劣弧FG,EH内,
∴)|cosα|>|sinα|的解集为{α|kπ-
<α<kπ+
,k∈Z}.

(1)∵在[0,2π)内,sin
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
OA,OB分别为
| π |
| 4 |
| 3π |
| 4 |
满足sinα≥
| ||
| 2 |
∴sinα≥
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |

(2)∵在[0,2π)内,cos
| π |
| 3 |
| 5π |
| 3 |
| 1 |
| 2 |
OC,OD分别为
| π |
| 3 |
| 5π |
| 3 |
满足cosα≤
| 1 |
| 2 |
∴cosα≤
| 1 |
| 2 |
| π |
| 3 |
| 5π |
| 3 |
(3)∵在[0,2π)内,|sin
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
| 7π |
| 4 |
| 7π |
| 4 |
| ||
| 2 |
OE,OF,OG,OH分别为
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| 7π |
| 4 |
满足cosα≤
| 1 |
| 2 |
∴)|cosα|>|sinα|的解集为{α|kπ-
| π |
| 4 |
| π |
| 4 |

点评:本题考查了三角函数线,考查了三角不等式的解法,考查了数形结合的解题思想方法,属于基本知识的考查.

练习册系列答案
相关题目
已知函数f(x)在定义在R上的奇函数,若对于任意给定的不等实数x1、x2,不等式x1f(x1)+x2f(x2)<x1f(x2)+x2f(x1)恒成立,则不等式f(x)<0的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,10) |
| D、(1,+∞) |