题目内容
7.若0<x<1,则$\frac{sinx}{x},{(\frac{sinx}{x})^2}$与$\frac{{sin{x^2}}}{x^2}$的大小关系为( )| A. | ${(\frac{sinx}{x})^2}<\frac{{sin{x^2}}}{x^2}<\frac{sinx}{x}$ | B. | $\frac{{sin{x^2}}}{x^2}<\frac{sinx}{x}<{(\frac{sinx}{x})^2}$ | ||
| C. | ${(\frac{sinx}{x})^2}<\frac{sinx}{x}<\frac{{sin{x^2}}}{x^2}$ | D. | $\frac{sinx}{x}<\frac{{sin{x^2}}}{x^2}<{(\frac{sinx}{x})^2}$ |
分析 先构造函数f(x)=x-sinx,根据导数判断sinx<x,再构造函数g(x)=$\frac{sinx}{x}$,根据导数求出函数的单调性,再利用单调性即可判断.
解答 解:令f(x)=x-sinx,0<x<1.
∴f′(x)=1-cosx>0,
函数f(x)单调递增.
∴f(x)>f(0)=0,
∴当x∈(0,1)时,
∴sinx<x
再g(x)=$\frac{sinx}{x}$,
则g′(x)=$\frac{xcosx-sinx}{{x}^{2}}$=$\frac{\frac{x-tanx}{{x}^{2}}}{cosx}$,
∵0<x<1<$\frac{π}{2}$<tanx
∴g′(x)<0,
故函数g(x)单调递减,
∴$\frac{{sin{x^2}}}{x^2}$<$\frac{sinx}{x}$<$\frac{{sin{x^2}}}{x^2}$,
故选:C
点评 本题考查导数和函数的单调性关系,以及比较大小的方法,关键时构造函数,属于中档题.

练习册系列答案
相关题目
18.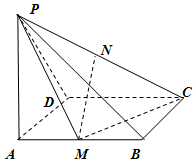 如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.
如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.
(1)求证:MN∥平面PAD;
(2)求证:MN⊥平面PCD;
(3)若PA=2,AB=4,求三棱锥B-PMC的体积.
 如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.
如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.(1)求证:MN∥平面PAD;
(2)求证:MN⊥平面PCD;
(3)若PA=2,AB=4,求三棱锥B-PMC的体积.
2.函数f(x)=$\left\{\begin{array}{l}{\sqrt{4-{x}^{2}}-2,(-2≤x<0)}\\{|{x}^{2}-x|,(x≤x≤2)}\end{array}\right.$的图象与x轴及x=±2所围成的封闭图形的面积为( )
| A. | 5-π | B. | 1+π | C. | π-3 | D. | 1-π |
12.命题“?x0∈∁RQ,x03∈Q”的否定是( )
| A. | ?x0∉∁RQ,x03∈Q | B. | ?x0∈∁RQ,x03∈Q | C. | ?x∉∁RQ,x3∈Q | D. | ?x∈∁RQ,x3∉Q |
19.已知数列{an}满足a1=1,a2=$\frac{2}{3}$ 且 $\frac{1}{{a}_{n+1}}$+$\frac{1}{{a}_{n-1}}$=$\frac{2}{{a}_{n}}$(n≥2),则a15等于( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{15}$ |
12.掷两枚均匀的骰子,已知点数不同,则至少有一个是3点的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |