题目内容
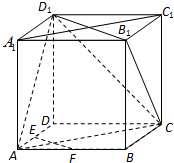
在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
| A、30° | B、60° |
| C、90° | D、120° |
考点:异面直线及其所成的角
专题:空间角
分析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线OP与AM所成的角的大小.
解答:
 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,A1P=t(0≤t≤1),
A(2,0,0),M(0,0,1)
O(1,1,0),P(2,t,2),
=(-2,0,1),
=(1,t-1,2),
∴
•
=-2+0+2=0,
∴异面直线OP与AM所成的角的大小为90°.
故选:C.
 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,A1P=t(0≤t≤1),
A(2,0,0),M(0,0,1)
O(1,1,0),P(2,t,2),
| AM |
| OP |
∴
| AM |
| OP |
∴异面直线OP与AM所成的角的大小为90°.
故选:C.
点评:本题考查异面直线OP与AM所成的角的大小的求法,是基础题,解题时要认真审题,注意向量法合理运用.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
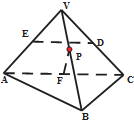 如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )
如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )| A、30° | B、60° |
| C、90° | D、随P点的变化而变化 |
若存在x∈[-2,3],使不等式4x-x2≥a成立,则实数a的取值范围是( )
| A、[-8,+∞) |
| B、[3,+∞) |
| C、(-∞,-12] |
| D、(-∞,4] |