题目内容
4.在平面直角坐标系xOy中,已知圆O:x2+y2=1,O1:(x-4)2+y2=4,动点P在直线x+$\sqrt{3}$y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是(-4,$\frac{20}{3}$).分析 求出P的轨迹方程,由动点P在直线x+$\sqrt{3}$y+b=0上,满足PB=2PA的点P有且只有两个,
转化为直线与圆x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0相交,即可求出实数b的取值范围.
解答 解:由题意O(0,0),O1(4,0),设P(x,y),则
∵PB=2PA,
∴(x-4)2+y2=4(x2+y2),
∴x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0,
其圆心坐标为(-$\frac{4}{3}$,0),半径为$\frac{8}{3}$;
∵动点P在直线x+$\sqrt{3}$y+b=0上,满足PB=2PA的点P有且只有两个,
∴该直线与圆x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0相交,
∴圆心到直线的距离满足d=$\frac{|-\frac{4}{3}+0+b|}{\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}}$<$\frac{8}{3}$,
化简得|b-$\frac{4}{3}$|<$\frac{16}{3}$,
解得-4<b<$\frac{20}{3}$,
∴实数b的取值范围是(-4,$\frac{20}{3}$).
故答案为:(-4,$\frac{20}{3}$).
点评 本题考查求点的轨迹方程以及直线与圆的位置关系的应用问题,正确转化是解题的关键,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知数列{an}的前n项和Sn=2an-1,则数列{an}的通项公式为( )
| A. | an=2n | B. | an=2n-1 | C. | an=2n-1 | D. | an=2n-1-1 |
12.已知log23=a,log25=b,则${log_2}\frac{9}{5}$=( )
| A. | $\frac{2a}{b}$ | B. | 2a-b | C. | a2-b | D. | $\frac{a^2}{b}$ |
16.某车间为了规定工时定额,需要确定加工零件所花费的时间,为些作了四次试验,得到的数据如下表所示:
(Ⅰ)求出y关于x的线性回归方程$\widehaty$=$\widehatbx$+$\widehata$,并在坐标系中画出回归直线;
(Ⅱ)试预测加工10个零件需要多少时间?b=$\frac{{\sum_{i=1}^n{({{x_1}-\overline x})({{y_1}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_1}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_1}{y_1}-n\overline{xy}}}}{{\sum_{i=1}^n{x_1^2-n{{\overline x}^2}}}}$,$\widehata$=$\overline y$-$\widehatb\overline x$,$\overline{x}$=$\frac{1}{n}\sum_{i=1}^n{x_1}$,$\overline y$=$\frac{1}{n}\sum_{i=1}^n{y_1}$.
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(Ⅱ)试预测加工10个零件需要多少时间?b=$\frac{{\sum_{i=1}^n{({{x_1}-\overline x})({{y_1}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_1}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_1}{y_1}-n\overline{xy}}}}{{\sum_{i=1}^n{x_1^2-n{{\overline x}^2}}}}$,$\widehata$=$\overline y$-$\widehatb\overline x$,$\overline{x}$=$\frac{1}{n}\sum_{i=1}^n{x_1}$,$\overline y$=$\frac{1}{n}\sum_{i=1}^n{y_1}$.
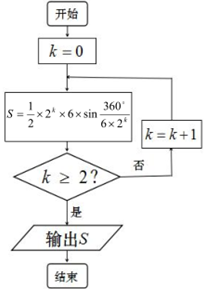 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近于圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的(四舍五入精确到小数点后两位)的值为( )(参考数据:sin15°=0.2588,sin75°=0.1305)
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近于圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的(四舍五入精确到小数点后两位)的值为( )(参考数据:sin15°=0.2588,sin75°=0.1305)