题目内容
8.依据三角函数线,作出如下四个判断,其中正确的是②④①sin $\frac{π}{6}$=sin$\frac{7π}{6}$; ②cos(-$\frac{π}{4}$)=cos$\frac{π}{4}$; ③tan$\frac{π}{8}$>tan$\frac{3π}{8}$; ④sin$\frac{3π}{5}$>sin $\frac{4π}{5}$.
分析 根据诱导公式、三角函数的单调性,判断各个选项是否正确,从而得出结论.
解答 解:①sin $\frac{π}{6}$=sin$\frac{7π}{6}$,错误,因为sin$\frac{7π}{6}$=-sin$\frac{π}{6}$=-$\frac{1}{2}$;
根据诱导共式,②cos(-$\frac{π}{4}$)=cos$\frac{π}{4}$正确;
根据y=tanx在(0,$\frac{π}{2}$)上单调递增,故③tan$\frac{π}{8}$>tan$\frac{3π}{8}$错误;
根据y=sinx在($\frac{π}{2}$,π) 上单调递减,可得④sin$\frac{3π}{5}$>sin $\frac{4π}{5}$正确.
故答案为:②④.
点评 本题主要考查诱导公式、三角函数的单调性,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
18.要得到函数f(x)=sin2x,x∈R,只需将函数g(x)=cos2x,x∈R的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
19.若方程mx2+(3-m)y2=1表示双曲线,则实数m的取值范围是( )
| A. | m<0 | B. | m>3 | C. | 0<m<3 | D. | m<0或m>3 |
3.定义在R上的函数f(x)的导函数为f'(x),f(x)的图象关于直线x=1对称,且(x-1)f'(x)<0,若x1<x2,且x1+x2>2,则f(x1)与f(x2)的大小关系是( )
| A. | f(x1)>f(x2) | B. | f(x1)<f(x2) | C. | f(x1)=f(x2) | D. | 不确定 |
13.一个几何体的三视图如图所示,其表面积为6π+$\sqrt{2}$π,则该几何体的体积为( )
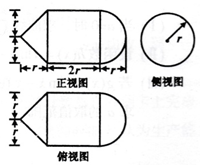

| A. | 4π | B. | 2π | C. | $\frac{11}{3}$π | D. | 3π |