题目内容
已知x=
是函数f（x）=asinx+cosx的一条对称轴，若（1-ax）2014=a0+a1x+a2x2+…+a2014x2014，则a1+a2+a3+…+a2014= ．
| π |
| 4 |
考点：二项式定理的应用
专题：三角函数的图像与性质,二项式定理
分析：利用x=
是函数f（x）的一条对称轴，求出a的值，再用赋值法求出a0+a1+a2+…+a2014的值．
| π |
| 4 |
解答：
解：∵x=
是函数f（x）=asinx+cosx的一条对称轴，
∴a=1；
∴（1-ax）2014=（1-x）2014=a0+a1x+a2x2+…+a2014x2014，
令x=1，则
（1-1）2014=a0+a1+a2+…+a2014=0，
∴a1+a2+a3+…+a2014=-1．
故答案为：-1．
| π |
| 4 |
∴a=1；
∴（1-ax）2014=（1-x）2014=a0+a1x+a2x2+…+a2014x2014，
令x=1，则
（1-1）2014=a0+a1+a2+…+a2014=0，
∴a1+a2+a3+…+a2014=-1．
故答案为：-1．
点评：本题考查了三角函数的图象与性质的应用问题，也考查了二项式定理的应用问题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
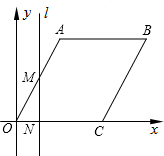如图，在平面直角坐标系中，四边形OABC是菱形，点C的坐标为（4，0），∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线l与菱形OABC的两边分别交于点M，N（点M在点N的上方），若△OMN的面积为S，直线l的运动时间为t秒（0≤t≤4），请求出S与t的函数关系．