题目内容
16.复数z满足(z-i)(2-i)=5,则z所对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由(z-i)(2-i)=5,得$z=\frac{6+2i}{2-i}$,然后利用复数代数形式的乘除运算化简复数z,求出z所对应的点的坐标,则答案可求.
解答 解:由(z-i)(2-i)=5,
得$z=\frac{6+2i}{2-i}$=$\frac{(6+2i)(2+i)}{(2-i)(2+i)}=\frac{10+10i}{5}=2+2i$,
则z所对应的点的坐标为:(2,2),位于第一象限.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
6.三棱柱ABC-A1B1C1的侧棱垂直于底面,且AB⊥BC,AB=BC=AA1=2,若该三棱柱的所有顶点都在同一球面上,则该球的表面积为( )
| A. | 48π | B. | 32π | C. | 12π | D. | 8π |
1.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,f($\frac{π}{2}$)=-1,则f(0)的值为( )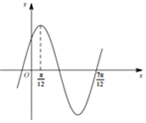

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
5.学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
| 销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
15.已知4cos(θ+$\frac{π}{3}$)cos(θ-$\frac{π}{6}$)=sin2θ,则tan(2θ-$\frac{π}{6}$)等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | -$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}}{3}$ |
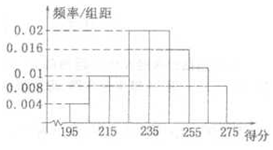 某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.
某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.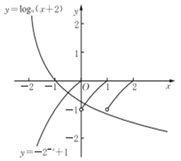 已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).
已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).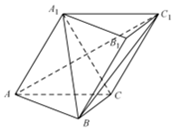 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.